IV. ОСНОВНЫЕ ПОНЯТИЯ ВОЛНОВОЙ
ОПТИКИ.
В монохроматической световой волне электрическое поле 
и магнитное поле 
изменяются
с постоянной частотой 
(циклическая частота),
каждая проекция векторов и пропорциональна
величине 
. Здесь 
-
время, 
- фаза колебаний, 
- начальная фаза, зависящая от пространственных
координат. Разные проекции векторов и могут иметь различающиеся начальные фазы.
В бегущей монохроматической световой волне векторы и
в каждый момент времени
перпендикулярны друг другу и равны по величине (в системе единиц СГС Гаусса).
Направление движения световой волны перпендикулярно обоим векторам и , то есть световая волна -
поперечная волна. Если векторы и в какой-то точке пространства в какой-то момент времени
не перпендикулярны друг другу или не равны по длине, то через эту точку
проходит не одна волна, а несколько волн в различных направлениях.
Далее будем обсуждать только направление распространения световой волны 
(вектор Пойнтинга) и направление вектора 
, так как направление вектора 
однозначно
ими определяется.
Пусть световая волна распространяется в направлении оси Z. Тогда вектор лежит в плоскости XY, так как перпендикулярен
направлению распространения. Если вектор колеблется
вдоль какой-то линии в этой плоскости, то световая волна называется линейно
поляризованной. Если вектор произвольно
меняется в плоскости XY, то в каждый момент времени его можно разложить на
сумму двух векторов вдоль осей X и Y. Произвольную волну, распространяющуюся
вдоль оси Z, можно представить, как сумму двух линейно поляризованных волн с
колебанием вектора вдоль осей X и Y
соответственно.
Если конец вектора вращается по окружности в
плоскости XY, то такой свет называется циркулярно поляризованным или светом с
круговой поляризацией. Свет поляризован по левому кругу, если в фиксированной
точке при наблюдении навстречу свету вектор (как и
вектор ) вращается по левому кругу, то есть
против часовой стрелки. Если конец вектора описывает
эллипс, то волна называется эллиптически поляризованной. Если волна
монохроматическая, то конец вектора описывает
эллипс, окружность, либо вектор гармонически
колеблется вдоль линии.
Интенсивностью световой волны 
называют среднее значение модуля вектора Пойнтинга.
Время усреднения либо считают равным времени регистрации света, либо равным
постоянной времени приемника света. Поскольку для бегущей волны векторы и перпендикулярны, модуль
вектора Пойнтинга можно найти по формуле 
. Если еще
учесть, что 
, то получим выражение 
. Следовательно для интенсивности можно записать 
, где скобки 
означают
среднее по времени значение. Эта формула приближенно верна и при сложении почти
однонаправленных световых волн.
При сложении двух или нескольких световых волн складываются не интенсивности волн, а напряженности и световых полей. При этом
если интенсивность суммы полей
отличается от суммы интенсивностей,
то говорят, что эти световые поля интерферируют. Если световые поля способны
интерферировать, то их называют когерентными друг другу.
Если на пути распространения световой волны встречается препятствие, то волна его огибает, поворачивает "за угол". Это явление называется дифракцией. Препятствием, например, может быть любой объект, который не пропускает, "загораживает", часть фронта световой волны.
V. ИНТЕРФЕРЕНЦИЯ.
Явление интерференции
состоит в том, что при сложении двух или нескольких световых волн, суммарная интенсивность света отличается от
суммы интенсивностей. Это
возможно потому, что складываются напряженности и световых волн, а интенсивность суммы световых волн
можно найти, в соответствии с определением интенсивности, по формуле (в системе единиц СГС Гаусса).
Интерференцию света обычно рассматривают не в одной точке, а на плоском экране. Поэтому говорят об интерференционной картине, под которой понимают чередующиеся полосы относительно большей и меньшей интенсивности света. Основными характеристиками интерференционной картины являются ширина полос интерференции и видность интерференционной картины.
Ширина интерференционных полос - это расстояние на экране между двумя соседними светлыми или двумя темными полосами.
Видность интерференционной картины по определению равна
Здесь 
- интенсивность света в середине
светлой полосы, 
- в середине ближайшей
темной полосы. Более строго можно ввести понятие видности, используя понятие
модуля комплексной степени когерентности
[2, 3].
Видность интерференционной
картины меняется в пределах от 0 до 1. Нулевая видность соответствует
условию 
, при котором полосы просто отсутствуют
(равномерно освещенная область экрана). Видность равная единице соответствует
условию 
.
Волны с ортогональными линейными поляризациями не интерферируют, так как для них интенсивность суммарной волны всегда равна сумме интенсивностей исходных волн. В том же смысле ортогональны лево и право циркулярно поляризованные волны.
Наиболее часто обсуждаемые в задачах по оптике поляризационные устройства -
поляризатор и фазовые пластинки 
и 
.
Поляризатор.
Идеальный поляризатор - это оптическое устройство, которое полностью пропускает одну линейную поляризацию и полностью поглощает ортогональную к ней поляризацию. Свет, распространяющийся в фиксированном направлении всегда можно мысленно представить как сумму двух линейно поляризованных во взаимно перпендикулярных направлениях волн, каждая из которых распространяется в том же направлении. Поляризатор оставляет одну из этих волн.
Пластинки и .
Плоскопараллельную фазовую пластинку или изготавливают из одноосного кристалла, так что
направление оси кристалла лежит в плоскости пластинки. Свет, падающий
перпендикулярно на фазовую пластинку, распространяется в ней в виде двух
независимых световых волн линейно поляризованных во взаимно перпендикулярных
направлениях. Поляризация (направление вектора 
)
обыкновенной волны перпендикулярна оси кристалла. Поляризация необыкновенной
волны совпадает с направлением оси кристалла.
Для каждой из двух волн кристалл имеет свой показатель преломления 
и 
. От показателя преломления зависит
оптическая толщина пластинки 
, где 
- геометрическая толщина. Поэтому две волны на выходе из
кристалла приобретают оптическую разность
хода 
. Если разность хода равна , то фазовая пластинка называется пластинкой . Если , то - . Подробнее понятие оптической
разности хода обсуждается в одном из следующих разделов.
Эта разность хода изменяет разность
фаз двух линейно поляризованных волн на величину 
.
Пластинка интересна тем, что она позволяет
получить циркулярно поляризованный свет из линейно поляризованного и наоборот. Чтобы
получить циркулярно поляризованный свет из линейно поляризованного, направление
линейной поляризации на входе пластинки должно
составлять угол 
с направлением оси кристалла
(свет падает перпендикулярно пластинке). Только в этом случае амплитуды
обыкновенной и необыкновенной волн в кристалле равны.
На входе в кристалл эти две волны синфазные в случае линейной поляризации
падающей волны. Тогда разности хода на выходе пластинки соответствует разность фаз 
. За пластинкой при сложении двух линейно поляризованных
волн с одинаковой амплитудой, взаимно ортогональной поляризацией и разностью
фаз образуется циркулярно поляризованная
волна.
Двухлучевая интерференция.
Под двухлучевой интерференцией понимают интерференционную картину, возникающую при сложении двух световых волн одинаковой частоты.
Рассмотрим простейшую задачу по интерференции.
Пусть две линейно поляризованные в одном направлении световые волны приходят в
одну точку экрана и имеют в этой точке зависимость напряженности электрического
поля от времени в виде: 
и 
.
Выразим интенсивность суммарной
световой волны 
через одинаковую интенсивность падающих световых
волн, которую обозначим 
, 
.
В этой задаче сумма интенсивностей
падающих волн равна 
. Интенсивность суммарной волны 
бывает как больше, так и меньше суммы интенсивностей в зависимости от
разности фаз интерферирующих волн. Светлая полоса (большая интенсивность) соответствует нулевой
разности фаз, темная - разности фаз равной 
.
При сложении двух волн одинаковой поляризации с интенсивностями 
и 
интенсивность суммарной волны
получаем аналогично:
.
Оптическая разность хода.
Вместо разности фаз 
интерферирующих волн удобно
ввести в рассмотрение пропорциональную ей величину 
-
оптическую разность хода, которая отличается множителем 
,
где 
- длина световой волны.
Изменению разности фаз на 
соответствует
изменение разности хода на .
В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода - это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.
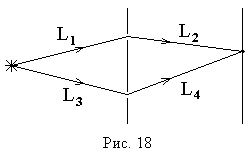Например, в оптической схеме
опыта Юнга, изображенной на рис. 18, разность хода для точки P на экране
находится по формуле:
.
В изотропной среде скорость света в 
раз
меньше, чем в вакууме, здесь - показатель преломления среды.
Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в раз меньше. В соответствии с соотношением вместо реального уменьшения длины волны можно рассматривать неизменную и
соответствующее увеличение длины пути луча. С этой целью вводится понятие
оптической длины пути, которая в раз больше
геометрической длины. Далее, употребляя термин "разность хода",
всегда будем иметь в виду оптическую разность хода.
Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины:
.
Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода.
Отметим, что разность хода лучей можно отсчитывать не только как разность
длин путей от источника до точки наблюдения, но и как разность длин путей от
двух точек любой поверхности равной фазы волны до точки наблюдения. При этом,
конечно, две точки на поверхности равной фазы - не произвольные точки, а должны
быть точками, через которые реально проходят лучи, попадающие в точку
наблюдения. Так на рис. 18 
, поэтому две щели
находятся на поверхности равной фазы, и, следовательно, разность хода можно
найти по упрощенной формуле 
. Этот прием часто
используется при решении задач.
Ширина интерференционных
полос.
Обычно экран для наблюдения интерференционной картины располагают так, чтобы оба луча и нормаль к экрану находились в одной плоскости. В этом случае ширина интерференционных полос полностью определяется углами падения световых волн на экран и длиной световой волны и не зависит от оптической схемы формирования интерферирующих волн.
Пусть две плоские световые
волны падают на экран под углами 
и 
(рис. 19), точки 
и 
- середины двух соседних светлых полос на экране, 
- поверхность равной фазы первой волны, 
- поверхность равной фазы второй волны. Поверхность имеет ту же фазу, что и поверхность , так как в точке фазы двух
волн одинаковые (светлая полоса). Поэтому можно считать, что это одна и та же
поверхность равной фазы волны, идущей от одного точечного источника разными
путями. Следовательно, оптическую разность
хода, например для точки экрана 
, можно
отсчитывать от пары точек 
и 
как бы общей поверхности равной фазы.
Из рис. 19 видно, что поверхность равной фазы 
первой
волны еще не дошла до точки 
на отрезок 
, а поверхность второй
волны уже зашла за точку на отрезок 
. Тогда оптическая
разность хода для точки равна
.
Точки и 
- середины
соседних светлых полос, тогда оптическая
разность хода равна длине волны 
, так как
при переходе по экрану на одну полосу разность
хода меняется на . Выражая из этого равенства
ширину полосы 
, и обозначая ее через 
, получаем
,
где знак '+' соответствует положительным углам падения 
и 
отсчитанным в разные стороны
от нормали к экрану, как на рис. 19.
В большинстве задач углы падения малы, тогда 
и
выражение для ширины полос упрощается
,
где 
- угол между лучами сходящимися на
экране.
Эта формула сводит оптическую задачу к геометрической. Для определения ширины интерференционных полос нужно построить два луча, выходящие из одной точки источника света и попадающие в одну точку экрана. Ширина полос - это отношение длины волны света к углу между лучами, сходящимися в одну точку.
Если ширины соседних полос заметно различаются, то термина "ширина
полос" избегают. Такая ситуация возникает при интерференции плоской и сферической волн,
например при наблюдении колец Ньютона. Кольца Ньютона наблюдаются при интерференции волны, отраженной от
сферической поверхности выпуклой линзы, и волны, отраженной от плоской
поверхности, соприкасающейся со сферической поверхностью линзы. В этой задаче
вместо ширины полос ищут радиус светлого (или темного) кольца с произвольным
номером 
.
Потеря полуволны.
В соответствии с формулами Френеля [2, 3] на границе раздела двух сред преломленная световая волна всегда в фазе с падающей волной, отраженная волна - либо в фазе, либо в противофазе. Иной сдвиг фазы отраженной волны возникает только в случае полного внутреннего отражения.
При нормальном падении света на границу раздела двух сред отраженная волна в
точке падения будет в противофазе с падающей при отражении от оптически более
плотной среды, от среды с более высоким показателем преломления.
Противоположная фаза отраженной волны эквивалентна сдвигу фазы на , или изменению разности
хода на 
. Поэтому говорят, что при отражении
от оптически более плотной среды происходит потеря полуволны. При этом в
выражении для оптической длины пути следует добавить (или вычесть) слагаемое 
.
Если одна из интерферирующих волн по пути к экрану испытала отражение с потерей полуволны, как, например, при наблюдении колец Ньютона в отраженном свете, то без учета потери полуволны в рассчитанной интерференционной картине темные полосы окажутся на месте светлых, а светлые - на месте темных.
Интерференция и закон сохранения энергии.
Совместим с помощью полупрозрачной пластинки две плоские световые волны одинаковой амплитуды, как показано на рис. 20. Тогда по формуле
можно найти интенсивность суммарной волны. Если
косинус в этом выражении равен (-1), то 
. Куда же
в таком случае делась энергия суммируемых волн? А если косинус равен (+1), то 
, что вдвое больше суммы интенсивностей суммируемых волн. Нет
ли здесь противоречия с законом сохранения энергии?
В действительности
противоречия нет, так как кроме сложения световых волн в направлении 
(рис. 21) происходит сложение волн в направлении 
. И при изменении величины косинуса в приведенной выше
формуле происходит перераспределение энергии между световыми волнами, идущими в
этих направлениях.
Для обоих направлений косинус будет принимать одно и тоже значение, и, если
больше света идет в направлении 
, то, казалось бы,
больше и в направлении 
. Противоречие с законом
сохранения энергии остается?
Положение спасает потеря
полуволны. Для плоскопараллельной полупрозрачной пластинки это не так очевидно,
из-за многократных отражений. Задача становится более простой в случае,
изображенном на рис. 22. Здесь полупространство вправо и вниз заполнено средой
с показателем преломления , а совмещение световых волн происходит при отражении и
преломлении света на границе среда - вакуум. Если в направлении 
отражение происходит с потерей полуволны, то в
направлении 
- без потери полуволны. Следовательно,
увеличение света в направлении 
сопровождается
уменьшением интенсивности света в
направлении 
. Таким образом, учет потери полуволны
устраняет противоречие. Данный способ совмещения световых волн (в направлении 
или в направлении 
)
называется способом деления амплитуды.
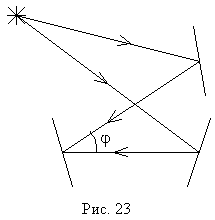Можно совмещать световые волны
другим способом, как это изображено на рис. 23. Этот метод наблюдения интерференции называют методом деления
волнового фронта.
В методе деления волнового фронта интерферирующие волны неизбежно
складываются под некоторым углом , что приводит к
появлению интерференционных
полос. Энергия световой волны при этом не возникает и не пропадает, она
перераспределяется между светлыми и темными интерференционными полосами.
Интересен случай, когда интерферирующие волны сходятся под малым углом , так что ширина
полос 
оказывается много больше ширины
интерферирующих пучков. Тогда, казалось бы, весь экран, на который попадает
весь свет, можно одновременно сделать темной интерференционной полосой или
одновременно светлой полосой.
В случае темной полосы,
например, энергия присутствует в каждой световой волне до совмещения волн, но
не доходит до экрана и не приходит вообще никуда.
Чтобы разобраться с этим вариантом парадокса необходимо учесть дифракцию волн. Попробуйте вернуться к его рассмотрению самостоятельно после изучения темы "Дифракция".