Методичка по оптике

Зоны Френеля.

Определить понятие зоны Френеля можно для дифракции на отверстии любой формы и даже вообще без отверстия, но практически полезно рассмотрение зон Френеля только при дифракции на круглом отверстии, причем в случае, когда источник света и точка наблюдения находятся на прямой, перпендикулярной к плоскости экрана с отверстием и проходящей через центр отверстия.

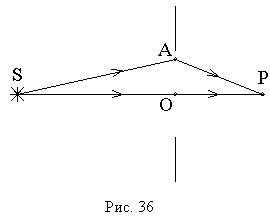Именно такой случай изображен на рис. 36. Здесь - точечный источник света, - точка наблюдения. На зоны Френеля можно мысленно разбить любую поверхность, через которую проходит свет, например, поверхность равной фазы. Но в нашем случае удобнее разбить на зоны Френеля плоскую поверхность отверстия.

Задача имеет ось симметрии, поэтому зоны Френеля имеют вид колец. Задача сводится к определению радиуса зоны Френеля с произвольным номером . Под радиусом зоны Френеля подразумевают больший радиус кольца.

Сделаем дополнительное построение (рис. 36). Соединим произвольную точку в плоскости отверстия отрезками прямых линий с источником света и с точкой наблюдения . Световая волна, которая приходит в точку наблюдения по пути , проходит больший путь, чем волна, прошедшая по пути . Разность хода определяет разность фаз волн, пришедших от вторичных источников и в точку наблюдения . От разности фаз зависит результат интерференции волн в точке и, следовательно, интенсивность света в этой точке.

Если разность хода равна , то свет приходит в точку наблюдения в противофазе. Следовательно, при разности хода меньше свет приходит более или менее в одинаковой фазе.

Это условие по определению является условием того, что точка находится в первой зоне Френеля. Тогда для границы первой зоны разность хода .

Это равенство позволяет найти радиус первой зоны, будем обозначать его . Он равен длине отрезка при разности хода .

Если оба расстояния и гораздо больше диаметра отверстия, а обычно рассматривают именно такой случай, то из геометрических соображений (рис. 36) можно получить

Аналогично, условие для внешней границы зоны Френеля с номером : . Откуда радиус -ой зоны Френеля

Отметим, что разбиение на зоны Френеля - это разбиение вторичного источника света на источники с одинаковой площадью, так как

От соседних зон Френеля свет приходит в противоположных фазах, так как разность хода от соседних зон по определению равна . Этот результат можно обобщить. Разбиение отверстия на кольца такие, что свет от соседних колец приходит в точку наблюдения с фиксированной разностью фаз, означает разбиение на кольца одинаковой площади. Можете доказать это в качестве задачи.

Рассмотрим теперь разбиение площади отверстия на гораздо более тонкие кольца равной площади. Эти кольца - вторичные источники света. Амплитуда света, пришедшего от каждого кольца в точку наблюдения примерно одинакова. Разность фаз света от соседних колец в точке тоже одинакова. Тогда комплексные амплитуды в точке наблюдения при сложении на комплексной плоскости образуют дугу окружности. Суммарная амплитуда - хорда.

Картина построения на комплексной плоскости совершенно аналогична картине для дифракции Фраунгофера на одной щели.

Рассмотрим теперь, как изменяется картина сложения комплексных амплитуд при изменении радиуса отверстия и сохранении остальных параметров задачи.

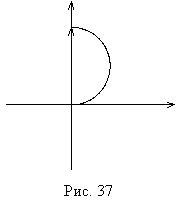Если отверстие открывает для точки наблюдения одну зону Френеля, то картина сложения амплитуд выглядит так, как изображено на рис. 37. Амплитуда от последнего тонкого кольца, повернута на угол относительно амплитуды от центральной части отверстия, так как соответствующая разность хода по определению первой зоны Френеля равна . Этот угол означает, что амплитуды образуют половину окружности.

Если отверстие открывает две зоны Френеля, то картина сложения амплитуд будет иметь вид окружности. В этом случае суммарная амплитуда света в точке равна нулю (нулевая длина хорды).

Если открыто три зоны Френеля, то картина представляет собой полторы окружности, и так далее.

Для четного числа зон Френеля амплитуда в точке наблюдения равна нулю. Для нечетного числа амплитуда одинаковая, максимальная и равна длине диаметра окружности на комплексной плоскости сложения амплитуд.

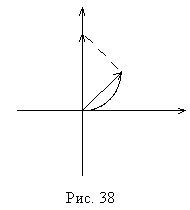Иногда в условии задачи говорится, что открыто какое-либо дробное число зон Френеля. При этом под половиной зоны Френеля понимают четверть окружности картины сложения амплитуд, что соответствует половине площади, а не радиуса, первой зоны Френеля. Аналогично для любого другого дробного числа зон Френеля. Для половины зоны Френеля, как видно из рис. 38, амплитуда поля в корень из двух раз меньше, чем для одной зоны Френеля.

Иногда в задачах говорится, что какое-то (дробное) число зон закрыто, затем сколько-то зон открыто и остальные закрыты. Тогда суммарную амплитуду поля можно найти, как векторную разность амплитуд двух задач.

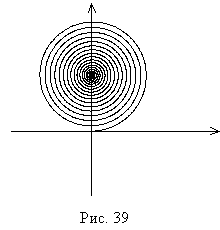Если открыты все зоны Френеля (нет препятствия на пути световой волны), то картина сложения амплитуд будет выглядеть как спираль, что очень грубо изображено на рис. 39. Спираль получается, потому что при большом числе открытых зон следует учитывать зависимость амплитуды света излученного вторичным источником от расстояния до точки наблюдения и от направления излучения вторичного источника. В результате, свет от зон с большим номером будет иметь малую амплитуду.

Центр спирали находится в середине окружности из первых двух зон, поэтому амплитуда поля при всех открытых зонах вдвое меньше, чем амплитуда поля при открытой одной первой зоне, а интенсивности различаются в четыре раза. Интенсивность света при открытой первой зоне Френеля в четыре раза больше интенсивности света перед экраном с отверстием.

В задачах на зоны Френеля обычно задана интенсивность света до экрана, в котором какие-то зоны Френеля открыты, какие-то - закрыты, и требуется найти интенсивность в точке наблюдения. Интенсивность - это квадрат амплитуды (с коэффициентом ). И заданная интенсивность света до экрана равна квадрату радиуса окружности на комплексной плоскости. Так если требуется найти отношение интенсивности света при открытой первой зоне к интенсивности падающей волны, то это отношение равно квадрату отношения диаметра окружности к ее радиусу.

В некоторых задачах рассматривается дифракция на небольшом непрозрачном экране, который закрывает для точки наблюдения небольшое число зон Френеля. Полезно сравнить эту задачу с дополнительной задачей, в которой эти зоны, наоборот, открыты, а все остальные - закрыты. Амплитуду поля в первой задаче можно найти, как векторную разность амплитуды исходной волны и амплитуды во второй задаче.

Дифракция Фраунгофера.

Дифракция Фраунгофера - это дифракция на отверстии, которое для точки наблюдения открывает заметно меньше одной зоны Френеля. Это условие выполнено, если точка наблюдения и источник света находятся достаточно далеко от отверстия.

Дифракция Френеля.

Дифракция Френеля - это дифракция в случае, когда отверстие открывает (или препятствие закрывает) для точки наблюдения несколько зон Френеля. Если открыто много зон Френеля, то дифракцией можно пренебречь, и мы оказываемся в приближении геометрической оптики.

Сравнение линзы и зонной пластинки.

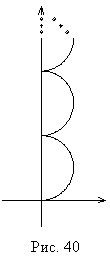Если закрыть все четные, или все нечетные, зоны Френеля, то в точке наблюдения будет свет с большой амплитудой. Действительно, каждая зона дает пол окружности на плоскости сложения комплексных амплитуд. Если оставить открытыми только нечетные зоны, то от общей спирали сложения амплитуд (рис. 39) останутся только половинки окружностей (рис. 40), дающие вклад "снизу вверх" в суммарную амплитуду поля.

Препятствие на пути световой волны, в котором открыты только четные или только нечетные зоны Френеля, называется зонной пластинкой. Интенсивность света в точке наблюдения за зонной пластинкой многократно превышает интенсивность света, падающего на зонную пластинку. Причина этого в том, что свет от каждой открытой зоны Френеля приходит в точку наблюдения в одной и той же фазе. Ситуация похожа на фокусировку света линзой.

Линза в отличии от зонной пластинки никакие зоны Френеля не закрывает, она сдвигает по фазе на свет от тех зон, которые закрывает зонная пластинка. За счет этого амплитуда света удваивается. Кроме того линза устраняет взаимные фазовые сдвиги световых волн, проходящих внутри одной зоны Френеля. Она разворачивает пол окружности на комплексной плоскости для каждой зоны Френеля в отрезок прямой линии. За счет этого амплитуда возрастает еще в раз. В результате всю спираль сложения комплексных амплитуд на комплексной плоскости линза разворачивает в прямую линию.

Как линза выравнивает фазы дифрагированных волн? Линза выравнивает оптическую длину пути различных лучей, от источника до изображения. Это, в свою очередь, возможно потому, что оптическая длина пути в стекле в раз больше геометрической длины.

Получение изображения точечного источника с помощью линзы можно рассматривать или по правилам геометрической оптики, или как результат дифракции и интерференции волн, проходящих через различные участки линзы. В последнем случае большая интенсивность света в точке изображения получается, как результат интерференции волн, прошедших через разные участки линзы и пришедших в точку изображения в одинаковой фазе. В другие точки за линзой свет приходит через различные участки линзы в различных фазах, поэтому интенсивность света в других точках намного меньше, чем в точке изображения.

Дифракционный предел разрешения.

В малой окрестности точки изображения интенсивность должна оставаться большой, так как разность хода и разность фаз при изменении точки наблюдения меняются непрерывно, а не скачком. Это приводит к тому, что на экране изображение точечного источника света не точка, а маленький светлый кружок. На границах кружка расфазировка дифрагированных волн становится порядка . Размер этого кружка можно формально найти если представить себе, что линза, как дырка в экране, приводит к дифракции на круглом отверстии. При дифракции плоской волны на круглом отверстии основная часть света идет в угол порядка , где - диаметр линзы. Угловой радиус первого темного кольца равен . Оказывается, что эта дифракционная расходимость не может быть скомпенсирована преломлением по законам геометрической оптики ни на какой сложной поверхности линзы. Поэтому плоская волна, например, собирается за линзой не в одну точку, а в кружок с радиусом , где - фокусное расстояние линзы.

Если сопряженная источнику света плоскость не совпадает с фокальной плоскостью линзы и находится на расстоянии , то дифракционный радиус кружка изображения точечного источника можно найти по формуле

Это основная формула, используемая при решении задач по теме "Дифракционный предел разрешения". Так предел углового разрешения телескопа, связан с тем, что изображение далекой звезды в фокальной плоскости линзы представляет собой кружок, а не точку. Принято считать (критерий Рэлея), что две звезды будут видны, как две, если центр кружка изображения одной звезды совпадает с первым темным кольцом дифракционного изображения второй звезды. В качестве задачи можете доказать, что это выполняется при угловом расстоянии между звездами, равном . Это и есть предел углового разрешения телескопа.

Аналогично примерно величине равен предел углового разрешения глаза и микроскопа. Для микроскопа обычно вместо углового разрешения рассматривают линейное разрешение - наименьшее расстояние между двумя "деталями" предмета, при котором микроскоп позволяет определить, что "детали" две, а не одна. Каждая мелкая "деталь" на экране вместо точки дает дифракционный кружок изображения. Если этот кружок по законам геометрической оптики отобразить на предмет, то его размер и будет примерно равен разрешению микроскопа . Предмет в микроскопе находится примерно на фокусном расстоянии от объектива, угловое дифракционное разрешение которого . Следовательно

где - входная апертура объектива.

Если между предметом и объективом среда с показателем преломления , то длина волны в среде в раз меньше, поэтому

Более строгая теория для некогерентного освещения объекта дает выражение

Величину называют числовой апертурой.

Явление дифракции также ограничивает спектральное разрешение спектрометра. Вспомните нормальную ширину щели.

Во всех случаях явление дифракции ограничивает угловое разрешение прибора величиной порядка , где - ширина пучка лучей.

VII. ЗАКЛЮЧЕНИЕ.

В заключении сделаем несколько замечаний о полезности применения соображений размерности.

Многие соотношения в оптике, как и вообще в физике, могут быть получены путем построения простейшей зависимости требуемых величин с учетом необходимой размерности результата.

Всевозможные малые углы можно выразить как отношение двух длин, одна из которых - длина волны , если угол от нее зависит. Так угол дифракции равен , где - размер препятствия; максимальная апертура интерференции - , где - размер источника света; угловой размер источника света - , где - длина пространственной когерентности; угол, под которым интерферирующие лучи сходятся на экране - , где - ширина полос интерференции.

Дифракционная решетка имеет три характерных линейных размера: - ширина прозрачной части штриха, - шаг решетки, - полная ширина решетки. Им соответствуют три характерных угла: - направление нулевой интенсивности дифракции на одной щели; - угол между главными максимумами дифракции; - угловая ширина главного максимума.

Частота и время - величины обратные. Обратная частота - это период колебаний ; единица деленная на спектральную ширину - время когерентности ; если излучение состоит из двух близких частот, то - период биений.

Если в зависимости сигнала от времени есть особенность с характерным временем , то в спектре сигнала есть особенность размером . Если свет встречает особенность с характерным линейным размером , то в распределении света по углам появляется особенность размером . И вообще, распределение света по углам - Фурье образ препятствия.

Подробнее смотрите литературу [2, 3].

VIII. ЛИТЕРАТУРА.

1. Козел С.М., Рашба Э.И., Славатинский С.А. Сборник задач по физике: Учеб. пособие - М.: Наука, 1987. 304с.

2. Бутиков Е.И. Оптика: Учеб. пособие для вузов/ Под ред. Н.И. Калитеевского.- М.: Высш. шк., 1986. 512с.

3. Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. 720с.