II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА.
Направление распространения света.
Направление движения энергии световой волны определяется вектором Пойнтинга ![]() (система единиц СГС Гаусса), здесь
(система единиц СГС Гаусса), здесь ![]() - скорость света в вакууме,
- скорость света в вакууме, ![]() и
и
![]() - векторные напряженности
электрического и магнитного полей. Длина вектора Пойнтинга равна плотности
потока энергии, то есть количеству энергии, которое в единицу времени протекает
через единичную площадку перпендикулярную вектору
- векторные напряженности
электрического и магнитного полей. Длина вектора Пойнтинга равна плотности
потока энергии, то есть количеству энергии, которое в единицу времени протекает
через единичную площадку перпендикулярную вектору ![]() .
В изотропной среде направление
.
В изотропной среде направление ![]() движения
поверхности фиксированной фазы совпадает с направлением
движения
поверхности фиксированной фазы совпадает с направлением ![]() движения
энергии световой волны. В кристалле эти направления могут не совпадать. Далее
будем рассматривать изотропную среду.
движения
энергии световой волны. В кристалле эти направления могут не совпадать. Далее
будем рассматривать изотропную среду.
Световые лучи.
Линии векторного поля ![]() , вдоль которых
распространяется свет, называются лучами. Если поверхности равных фаз
представляют собой параллельные плоскости, то волна называется плоской. Плоской
волне соответствует параллельный пучок лучей, так как лучи в изотропной среде
перпендикулярны поверхностям равных фаз. Сферической волной называется волна с
поверхностями равных фаз сферической формы. Ей соответствует пучок лучей,
выходящих из одной точки или собирающихся в одну точку. В этих двух случаях
говорят соответственно о расходящейся и о сходящейся сферической волне.
, вдоль которых
распространяется свет, называются лучами. Если поверхности равных фаз
представляют собой параллельные плоскости, то волна называется плоской. Плоской
волне соответствует параллельный пучок лучей, так как лучи в изотропной среде
перпендикулярны поверхностям равных фаз. Сферической волной называется волна с
поверхностями равных фаз сферической формы. Ей соответствует пучок лучей,
выходящих из одной точки или собирающихся в одну точку. В этих двух случаях
говорят соответственно о расходящейся и о сходящейся сферической волне.
Приближение геометрической
оптики.
Если длина световой волны очень мала по сравнению со всеми размерами оптических приборов, то явлениями дифракции и интерференции можно пренебречь. Такое рассмотрение распространения света называется приближением геометрической оптики.
Геометрическая оптика обычно ограничивается рассмотрением распространения света в однородных средах и предметах, состоящих из однородных сред. Распространение света в среде с плавно изменяющимся показателем преломления описывается уравнением эйконала.
Отражение и преломление
света.
 Если
световая волна распространяется в однородной среде без препятствий, то
волна распространяется по прямым линиям - лучам. На границе раздела двух
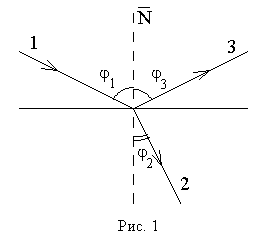
однородных сред лучи отражаются и преломляются (рис.1). Отраженный (3) и
преломленный (2) лучи находятся в одной плоскости с падающим лучом (1) и
перпендикуляром к границе раздела двух сред (
Если
световая волна распространяется в однородной среде без препятствий, то
волна распространяется по прямым линиям - лучам. На границе раздела двух
однородных сред лучи отражаются и преломляются (рис.1). Отраженный (3) и
преломленный (2) лучи находятся в одной плоскости с падающим лучом (1) и
перпендикуляром к границе раздела двух сред (![]() ). Угол
падения
). Угол
падения ![]() равен углу отражения
равен углу отражения ![]() . Угол преломления
. Угол преломления ![]() можно
найти из равенства
можно
найти из равенства
![]() ,
,
где ![]() и
и ![]() - показатели преломления первой и
второй среды.
- показатели преломления первой и
второй среды.
Отражение от плоского
зеркала.
Плоское зеркало, как и сферическое, отражает лучи света в соответствии с законом отражения (угол падения равен углу отражения). Свет после отражения от плоского зеркала во всех смыслах распространяется так, как если бы вместо зеркала стояло окошко, а источник света располагался бы за поверхностью зеркала, за окошком. Интересно, что изображение в зеркале находится не просто в другом месте, оно вывернуто "наизнанку", при этом "правое" и "левое" меняются местами. Например, правая спираль становится левой спиралью.
Преломление света, также как и отражение, можно рассматривать, как "кажущееся" изменение положения источника света. Этот факт проявляется в кажущемся изломе прямой палки, наполовину опущенной в воду под углом к поверхности воды. Мнимое положение источника света в данном случае будет различаться для лучей, падающих на границу раздела двух сред под различными углами. По этой причине обычно избегают говорить о мнимом положении источника света при преломлении.
Призма.
В задачах с призмами поворот света призмой можно рассматривать как два последовательных преломления света на плоских гранях призмы при входе света в призму и при его выходе.
 Особый интерес представляет
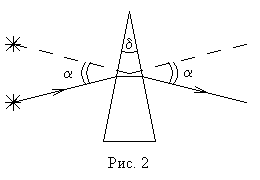
частный случай призмы с малым углом при вершине (
Особый интерес представляет
частный случай призмы с малым углом при вершине (![]() на рис. 2). Такую призму называют тонкой призмой. Обычно рассматриваются
задачи, в которых свет падает на тонкую призму почти перпендикулярно ее
поверхности. При этом за два преломления лучи света поворачивают на малый угол
на рис. 2). Такую призму называют тонкой призмой. Обычно рассматриваются
задачи, в которых свет падает на тонкую призму почти перпендикулярно ее
поверхности. При этом за два преломления лучи света поворачивают на малый угол ![]() в плоскости перпендикулярной ребру призмы в сторону
утолщения призмы (рис. 2). Угол поворота не зависит от угла падения света в
приближении малых углов падения. Это означает, что призма поворачивает
"кажущееся" положение источника света на угол
в плоскости перпендикулярной ребру призмы в сторону
утолщения призмы (рис. 2). Угол поворота не зависит от угла падения света в
приближении малых углов падения. Это означает, что призма поворачивает
"кажущееся" положение источника света на угол ![]() в
плоскости перпендикулярной ребру призмы.
в
плоскости перпендикулярной ребру призмы.
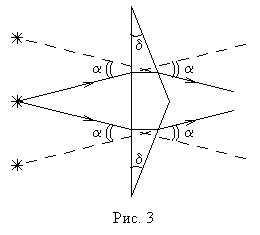 Из двух таких тонких призм
состоит, в частности, бипризма Френеля (рис. 3), проходя через которую свет от
точечного источника распространяется далее так, как если бы свет излучался
двумя точечными когерентными
источниками.
Из двух таких тонких призм
состоит, в частности, бипризма Френеля (рис. 3), проходя через которую свет от
точечного источника распространяется далее так, как если бы свет излучался
двумя точечными когерентными
источниками.
Оптическая ось.
Оптической осью называется прямая линия, проходящая через центры кривизны отражающих и преломляющих поверхностей. Если система имеет оптическую ось, то это центрированная оптическая система [2].
Линза.
Обычно прохождение света через линзу рассматривается в приближении параксиальной оптики, это означает, что направление распространения света всегда составляет малый угол с оптической осью, и лучи пересекают любую поверхность на малом расстоянии от оптической оси.
Линза может быть собирающей или рассеивающей.
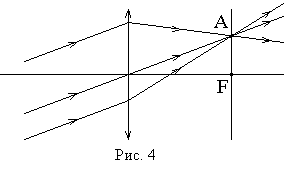 Лучи,
параллельные оптической оси, после собирающей линзы проходят через одну и
ту же точку. Эта точка называется фокусом линзы. Расстояние от линзы до ее
фокуса называется фокусным расстоянием. Плоскость, перпендикулярная оптической
оси и проходящая через фокус линзы, называется фокальной плоскостью.
Параллельный пучок лучей, наклоненный к оптической оси, собирается за линзой в
одну точку (
Лучи,
параллельные оптической оси, после собирающей линзы проходят через одну и
ту же точку. Эта точка называется фокусом линзы. Расстояние от линзы до ее
фокуса называется фокусным расстоянием. Плоскость, перпендикулярная оптической
оси и проходящая через фокус линзы, называется фокальной плоскостью.
Параллельный пучок лучей, наклоненный к оптической оси, собирается за линзой в
одну точку (![]() на рис. 4) в фокальной плоскости
линзы.
на рис. 4) в фокальной плоскости
линзы.
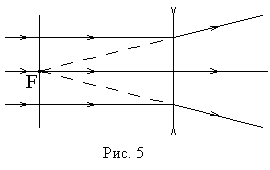 Рассеивающая линза преобразует
параллельный оптической оси пучок лучей в расходящийся пучок (рис. 5). Если
расходящиеся лучи продолжить назад, то они пересекутся в одной точке
Рассеивающая линза преобразует
параллельный оптической оси пучок лучей в расходящийся пучок (рис. 5). Если
расходящиеся лучи продолжить назад, то они пересекутся в одной точке ![]() - фокусе рассеивающей
линзы. При небольшом повороте пучка параллельных лучей точка пересечения
перемещается по фокальной плоскости рассеивающей линзы.
- фокусе рассеивающей
линзы. При небольшом повороте пучка параллельных лучей точка пересечения
перемещается по фокальной плоскости рассеивающей линзы.
Построение изображений.
В задачах на построение изображений подразумевается, что протяженный источник света состоит из некогерентных точечных источников. В этом случае изображение протяженного источника света состоит из изображений каждой точки источника, полученных независимо друг от друга.
Изображение точечного источника - это точка пересечения всех лучей после
прохождения через систему, лучей испущенных точечным источником света. Точечный
источник испускает сферическую световую волну. В приближении параксиальной
оптики сферическая волна, проходя через линзу (рис. 6), распространяется и далее
в виде сферической волны, но с другим значением радиуса кривизны. Лучи за
линзой либо сходятся в одну точку (рис. 6а), которую называют действительным
изображением источника (точка ![]() ), либо расходятся
(рис. 6б). В последнем случае продолжения лучей назад пересекаются в некоторой
точке
), либо расходятся
(рис. 6б). В последнем случае продолжения лучей назад пересекаются в некоторой
точке ![]() , которая называется мнимым
изображением источника света.
, которая называется мнимым
изображением источника света.
В параксиальном приближении все лучи, исходящие из одной точки до линзы, после линзы пересекаются в одной точке, поэтому для построения изображения точечного источника достаточно найти точку пересечения "удобных нам" двух лучей, эта точка и будет изображением.
Если перпендикулярно оптической оси поставить лист бумаги (экран) так, чтобы изображение точечного источника попало на экран, то в случае действительного изображения на экране будет видна светящаяся точка, а в случае мнимого изображения - нет.
Построение изображения в
тонкой линзе.
Есть три луча, удобных для построения изображения точечного источника света в тонкой линзе.
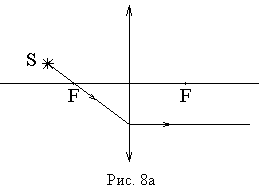
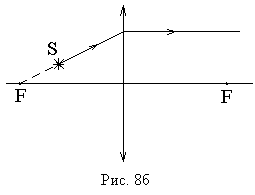
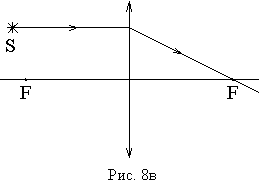
Первый луч проходит через центр линзы. После линзы он не изменяет своего направления (рис. 7) как для собирающей так и для рассеивающей линзы. Это справедливо только в том случае, если среда с обеих сторон линзы имеет одинаковый показатель преломления. Два других удобных луча рассмотрим на примере собирающей линзы. Один из них проходит через передний фокус (рис. 8а), или его продолжение назад проходит через передний фокус (рис. 8б). После линзы такой луч пойдет параллельно оптической оси. Другой луч проходит до линзы параллельно оптической оси, а после линзы через задний фокус (рис. 8в).
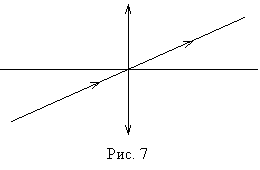
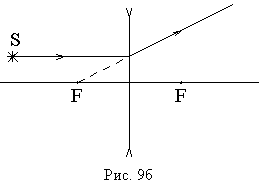
Удобные для построения изображения лучи в случае рассеивающей линзы показаны на рис. 9а,9б.
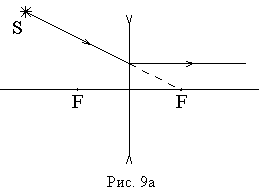
Точка пересечения, мнимого или действительного, любой пары из этих трех лучей, прошедших линзу, совпадает с изображением источника.
В задачах по оптике иногда возникает потребность найти ход луча не для одного из удобных нам трех лучей, а для произвольного луча (1 на рис. 10), направление которого до линзы определено условиями задачи.
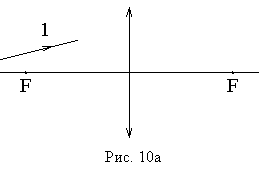 В таком случае полезно
рассмотреть, например, параллельный ему луч (2 на рис. 10б), проходящий через
центр линзы, независимо от того есть или нет такой луч на самом деле.
В таком случае полезно
рассмотреть, например, параллельный ему луч (2 на рис. 10б), проходящий через
центр линзы, независимо от того есть или нет такой луч на самом деле.
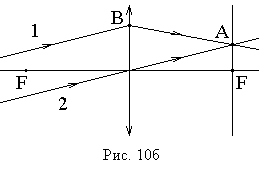 Параллельные лучи собираются
за линзой в фокальной плоскости. Эту точку (
Параллельные лучи собираются
за линзой в фокальной плоскости. Эту точку (![]() на рис.
10б) можно найти как точку пересечения фокальной плоскости и вспомогательного
луча 2, проходящего линзу без изменения направления. Вторая точка, необходимая
и достаточная для построения хода луча 1 после линзы, это точка на тонкой линзе
(
на рис.
10б) можно найти как точку пересечения фокальной плоскости и вспомогательного
луча 2, проходящего линзу без изменения направления. Вторая точка, необходимая
и достаточная для построения хода луча 1 после линзы, это точка на тонкой линзе
(![]() на рис. 10б), в которую упирается луч
1 с той стороны, где его направление известно.
на рис. 10б), в которую упирается луч
1 с той стороны, где его направление известно.
Построение изображения в
толстой линзе.
Тонкая линза - линза, толщина которой много меньше ее фокусного расстояния. Если линзу нельзя считать тонкой, то каждую из двух сферических поверхностей линзы можно рассматривать как отдельную тонкую линзу.
Тогда изображение в толстой линзе можно найти как изображение изображения. Первая сферическая поверхность толстой линзы дает изображение источника как изображение в тонкой линзе. Вторая сферическая поверхность дает изображение этого изображения.
Другой подход при построении изображений состоит в том, что вводится понятие главных плоскостей центрированной оптической системы, частным случаем которой может быть толстая линза. Центрированная оптическая система, которая может состоять и из большого числа линз, полностью характеризуется двумя фокальными и двумя главными плоскостями. Полностью характеризуется в том смысле, что знание положения этих четырех плоскостей достаточно для построения изображений. Все четыре плоскости перпендикулярны оптической оси, следовательно свойства оптической системы полностью определяются четырьмя точками пересечения четырех плоскостей с оптической осью. Эти точки называются кардинальными точками системы.
Для тонкой линзы обе главные плоскости совпадают с положением самой линзы. Для более сложных оптических систем существуют формулы расчета положения кардинальных точек через радиусы кривизны поверхностей линз и показатели их преломления [2].
Для построения изображения точечного источника достаточно рассмотреть прохождение через оптическую систему двух удобных нам лучей и найти точку их пересечения после линзы, либо точку пересечения продолжений лучей назад (для мнимого изображения).
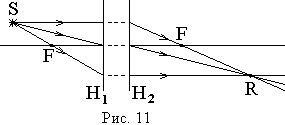
Построение хода лучей проводится так, как будто между главными плоскостями
системы находится тонкая линза, а пространство между главными плоскостями
отсутствует. Пример построения приведен на рис. 11. ![]() и
и
![]() - главные плоскости системы.
- главные плоскости системы.
 Задача прохождения света через
центрированную оптическую систему может быть решена не только геометрическим
построением хода лучей, но и аналитически. Для аналитического решения задач
удобен матричный метод [2].
Задача прохождения света через
центрированную оптическую систему может быть решена не только геометрическим
построением хода лучей, но и аналитически. Для аналитического решения задач
удобен матричный метод [2].
Формулы тонкой линзы.
Если в задаче требуется аналитический результат, а не построение изображения, то для решения обычно достаточно трех формул:
![]()
![]()
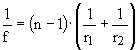 .
.
Здесь ![]() - оптическая сила линзы,
- оптическая сила линзы, ![]() - фокусное расстояние,
- фокусное расстояние, ![]() - расстояние от линзы до источника света,
- расстояние от линзы до источника света, ![]() - расстояние от линзы до изображения,
- расстояние от линзы до изображения, ![]() и
и ![]() - радиусы кривизны обоих
поверхностей линзы,
- радиусы кривизны обоих
поверхностей линзы, ![]() - показатель преломления материала
линзы.
- показатель преломления материала
линзы.
В этих формулах все величины с размерностью длины могут принимать как
положительные, так и отрицательные значения. Фокусное
расстояние ![]() положительно для собирающей линзы,
положительно для собирающей линзы, ![]() положительно для действительного изображения,
положительно для действительного изображения, ![]() и
и ![]() положительны для
двояковыпуклой линзы. Расстояние от линзы до источника - положительная
величина, но и тут можно представить себе мнимый точечный источник, для
которого это расстояние будет отрицательным.
положительны для
двояковыпуклой линзы. Расстояние от линзы до источника - положительная
величина, но и тут можно представить себе мнимый точечный источник, для
которого это расстояние будет отрицательным.
Реже встречаются задачи, в которых показатели преломления среды с двух сторон от линзы различаются. Тогда потребуются следующие формулы:
![]()
Может быть полезна и формула для оптической силы одной сферической поверхности, в частности при рассмотрении толстой линзы как двух сферических поверхностей:
![]()
Сферическое зеркало.
Чтобы удовлетворить приближению параксиальной оптики, нужно потребовать, чтобы сферическое зеркало было малой частью сферы. Другими словами, размер зеркала должен быть много меньше радиуса кривизны сферы.
Сферическое зеркало отражает световые лучи аналогично оптической системе, состоящей из тонкой линзы и вплотную поставленного плоского зеркала. Вогнутое зеркало аналогично собирающей линзе, выпуклое - рассеивающей.
Модуль фокусного расстояния сферического зеркала равен половине радиуса кривизны сферы
![]()
Фокус расположен посередине между зеркалом и центром сферы.
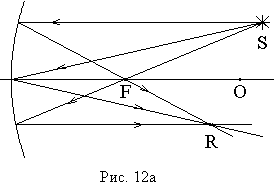
На рис. 12а,б приведены примеры построения изображений точечного источника света в сферическом зеркале.