III закон Ньютона
III закон Ньютона
По III закону Ньютона сила F, действующая на тело, является проявлением взаимодействия с некоторым источником, причем само тело действует на источник с силой F’, равной F и направленной в противоположную сторону: F= — F’. Для центрально-симметричных взаимодействий силы действия и противодействия всегда направлены по одной прямой. В общем случае эти силы направлены как показано на рис. A1
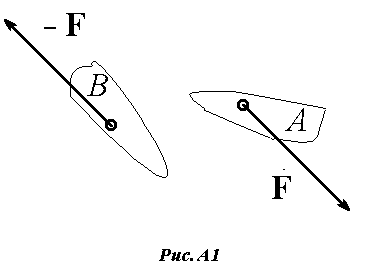
не по линии, соединяющей точки приложения этих сил, а по параллельным линиям. При этом оказывается, что суммарный момент сил в системе двух взаимодействующих тел A и B отличен от нуля!
Докажем, что отличный от нуля момент сил, действующих на некоторую систему из N тел, приводит к изменению ее момента количества движения.
Выпишем уравнения движения для каждого из N тел в следующем виде:
Введенные здесь обозначения очевидны:
Fi — суммарная сила, действующая на тело i;
vi и pi — скорость и импульс этого тела в данный момент;
Dt — промежуток времени, малый настолько, чтобы можно было пренебречь изменением любых параметров системы.
Умножим равенство (A1) слева векторно на радиус-вектор точки приложения силы Fi:
Правую часть этого равенства можно переписать в виде
так как имеет место тождество
Последнее слагаемое в правой части этого тождества обращается в ноль в виду того, что D ri||pi (векторное произведение параллельных векторов равно нулю).
Проведем в (A2) суммирование по i:
В левой части этого равенства стоит импульс суммарного момента сил M, а в правой - изменение суммарного момента количества движения L всей системы:
Из этого равенства следует, что отличный от нуля момент сил приводит к изменению вектора момента количества движения системы.
В системе двух тел, изображенной на рис. A1, суммарный момент сил отличен от нуля. Такая система должна, в соответствии с формулой (A3), ускоренно вращаться относительно общего центра масс, что противоречит, в частности, закону сохранения энергии. Могут ли существовать системы, подобные изображенной на рис. A1?
Сила, действующая на частицу в потенциальном поле, равна
где введен векторный оператор градиента
.Для центрального-симметричного потенциального поля потенциал взаимодействия двух частиц зависит (по определению) только от расстояния между ними: U(r1, r2)=U(|r1- r2|). Следовательно, силы взаимодействия частиц F1 и F2 равны:
Здесь
.Обозначим |r1- r2|=r и заметим, что
Таким образом, для центрально-симметричных потенциалов силы действия и противодействия всегда направлены по одной линии в противоположенные стороны. В природе центрально-симметричные потенциалы описывают все дальнодействующие поля - гравитационное и электростатическое. Нецентральные поля (ядерные) имеют конечный радиус взаимодействия (-13см) и не проявляются в макроскопической физике.
Тем не менее центрально-симметричные потенциалы могут приводить к нецентральным взаимодействиям. Приведем конкретный пример такой системы. Заряд q расположим на расстоя нии L от середины диполя, состоящего из зарядов +q и -q, как показано на рис. A2. Дл ина диполя dL.
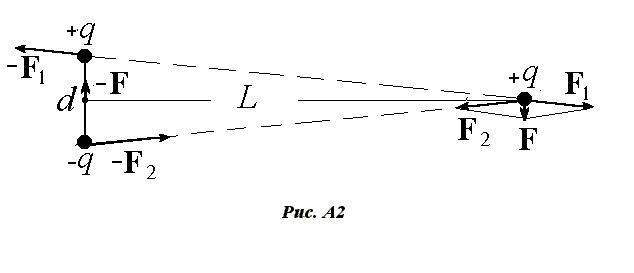
Силы F1 и F2, действующие на заряд со стороны диполя, равны по величине. Их векторная сумма равна F. Силы, действующие на диполь со стороны заряда, равны -F1 и -F2 соответственно, а их сумма -F. Момент сил F и -F относительно любой точки отличен от нуля, направле н по часовой стрелке и равен M=FL. Но заметим, что момент сил -F1 и -F2, п риложенных к диполю, тоже отличен от нуля, направлен против часовой стрелки и равен M’@ F1d. Из сравнения треугольника сил F1, F2, F с треугольником, в вершинах которого находятся заряды, видим, что F 1/F@ L/d. Отсюда получаем, что F1d @ FL и M=M’, а в векторной форме M=- M’. Следовательно, суммарный момент сил, действующих в этой системе, равен нулю.
Заряд, находящийся в точке B, действуя на диполь, расположенный в точке A, создает не только силу - F, но и момент сил - M’.
Покажем, что потенциальное поле, создаваемое диполем, нецентральное.
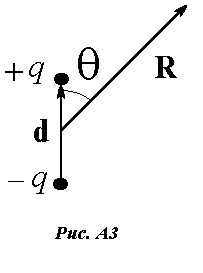
Для этого обратимся к рис. А3 и вычислим потенциал в произвольной точке на расстоянии R от центра диполя под углом q к вектору d, соединяющему заряды диполя:
Это выражение на расстояниях R>>d можно упростить, используя разложение по малой величине d/R:
С учетом этого приближения формула (A8) может быть переписана в виде
Для элементарного диполя d- 0, q стремится к бесконечности при фиксированном значении дипольного момента p=qd. Потенциал поля такого диполя
Видим, что потенциальное поле диполя не обладает сферической симметрией — потенциал явно зависит не только от расстояния R до диполя, но и от угла q между осью диполя и направлением в точку наблюдения.
Таким образом, даже в центрально-симметричных потенциальных полях взаимодействие элементарных объектов может иметь вид, характерный для нецентральных потенциалов. Силы действия и противодей ствия равны, направлены противоположно, но не по одной прямой, соединяющей точки приложения сил, а по параллельным линиям. При этом взаимодействие в целом описывается не только силами, но и моментами сил, т. е. имеет более сложный вид, чем обычно подразумевается при формулировке III закона.
III закон Ньютона
III закон Ньютона
По III закону Ньютона сила F, действующая на тело, является проявлением взаимодействия с некоторым источником, причем само тело действует на источник с силой F’, равной F и направленной в противоположную сторону: F= — F’. Для центрально-симметричных взаимодействий силы действия и противодействия всегда направлены по одной прямой. В общем случае эти силы направлены как показано на рис. A1
не по линии, соединяющей точки приложения этих сил, а по параллельным линиям. При этом оказывается, что суммарный момент сил в системе двух взаимодействующих тел A и B отличен от нуля!
Докажем, что отличный от нуля момент сил, действующих на некоторую систему из N тел, приводит к изменению ее момента количества движения.
Выпишем уравнения движения для каждого из N тел в следующем виде:
Введенные здесь обозначения очевидны:
Fi — суммарная сила, действующая на тело i;
vi и pi — скорость и импульс этого тела в данный момент;
Dt — промежуток времени, малый настолько, чтобы можно было пренебречь изменением любых параметров системы.
Умножим равенство (A1) слева векторно на радиус-вектор точки приложения силы Fi:
Правую часть этого равенства можно переписать в виде
так как имеет место тождество
Последнее слагаемое в правой части этого тождества обращается в ноль в виду того, что D ri||pi (векторное произведение параллельных векторов равно нулю).
Проведем в (A2) суммирование по i:
В левой части этого равенства стоит импульс суммарного момента сил M, а в правой - изменение суммарного момента количества движения L всей системы:
Из этого равенства следует, что отличный от нуля момент сил приводит к изменению вектора момента количества движения системы.
В системе двух тел, изображенной на рис. A1, суммарный момент сил отличен от нуля. Такая система должна, в соответствии с формулой (A3), ускоренно вращаться относительно общего центра масс, что противоречит, в частности, закону сохранения энергии. Могут ли существовать системы, подобные изображенной на рис. A1?
Сила, действующая на частицу в потенциальном поле, равна
где введен векторный оператор градиента
.Для центрального-симметричного потенциального поля потенциал взаимодействия двух частиц зависит (по определению) только от расстояния между ними: U(r1, r2)=U(|r1- r2|). Следовательно, силы взаимодействия частиц F1 и F2 равны:
Здесь
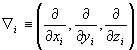.Обозначим |r1- r2|=r и заметим, что
Таким образом, для центрально-симметричных потенциалов силы действия и противодействия всегда направлены по одной линии в противоположенные стороны. В природе центрально-симметричные потенциалы описывают все дальнодействующие поля - гравитационное и электростатическое. Нецентральные поля (ядерные) имеют конечный радиус взаимодействия (-13см) и не проявляются в макроскопической физике.
Тем не менее центрально-симметричные потенциалы могут приводить к нецентральным взаимодействиям. Приведем конкретный пример такой системы. Заряд q расположим на расстоянии L от середины диполя, состоящего из зарядов +q и -q, как показано на рис. A2. Дл ина диполя dL.
Силы F1 и F2, действующие на заряд со стороны диполя, равны по величине. Их векторная сумма равна F. Силы, действующие на диполь со стороны заряда, равны -F1 и -F2 соответственно, а их сумма -F. Момент сил F и -F относительно любой точки отличен от нуля, направле н по часовой стрелке и равен M=FL. Но заметим, что момент сил -F1 и -F2, п риложенных к диполю, тоже отличен от нуля, направлен против часовой стрелки и равен M’@ F1d. Из сравнения треугольника сил F1, F2, F с треугольником, в вершинах которого находятся заряды, видим, что F 1/F@ L/d. Отсюда получаем, что F1d @ FL и M=M’, а в векторной форме M=- M’. Следовательно, суммарный момент сил, действующих в этой системе, равен нулю.
Заряд, находящийся в точке B, действуя на диполь, расположенный в точке A, создает не только силу - F, но и момент сил - M’.
Покажем, что потенциальное поле, создаваемое диполем, нецентральное.
Для этого обратимся к рис. А3 и вычислим потенциал в произвольной точке на расстоянии R от центра диполя под углом q к вектору d, соединяющему заряды диполя:
Это выражение на расстояниях R>>d можно упростить, используя разложение по малой величине d/R:
С учетом этого приближения формула (A8) может быть переписана в виде
Для элементарного диполя d- 0, q стремится к бесконечности при фиксированном значении дипольного момента p=qd. Потенциал поля такого диполя
Видим, что потенциальное поле диполя не обладает сферической симметрией — потенциал явно зависит не только от расстояния R до диполя, но и от угла q между осью диполя и направлением в точку наблюдения.
Таким образом, даже в центрально-симметричных потенциальных полях взаимодействие элементарных объектов может иметь вид, характерный для нецентральных потенциалов. Силы действия и противодей ствия равны, направлены противоположно, но не по одной прямой, соединяющей точки приложения сил, а по параллельным линиям. При этом взаимодействие в целом описывается не только силами, но и моментами сил, т. е. имеет более сложный вид, чем обычно подразумевается при формулировке III закона.
Закон Архимеда для ускоренно движущихся тел
С. Н. Манида
Установлена зависимость силы гидростатического давления (силы Архимеда) от плотности свободного тела, погруженного в жидкость.
1. Закон Архимеда для неподвижных тел
Любое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.
Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.
Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью 
действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (gh) и не зависящая от ориентации поверхности.
Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С помощью современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление этого ученого, когда окажется, что полученный результат численно равен весу жидкост и в объеме погруженной части тела! Этот результат был получен греческим ученым Архимедом 2200 лет назад, причем в общем виде — для тел любой формы!
Попробуем восстановить ход рассуждений Архимеда и вывести его закон.
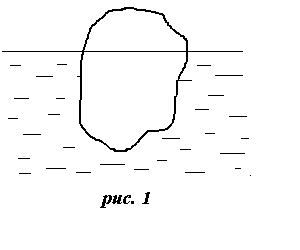
На рис. 1, изображено тело, помещенное в жидкость. На это тело со стороны жидкости действует описанная выше сила гидростатического давления. Для нахождения этой силы вместо вычисления сложных интегралов проведем мысленный эксперимент: уберем тело и рассмотрим жидкость в объеме V, который занимала погруженная часть тела (рис. 2). На эту жидкость действует сила тяжести Vg и сила гидростатического давления F. Выделенный объем находится в равновесии, следовательно, сумма сил, действующих на жидкость в этом объеме, равна нулю: F+ Vg =0.
Отсюда следует выражение для силы гидростатического давления: F=-Vg.
Мы нашли силу, действующую на поверхность жидкости, заполняющей объем V. Но поверхность тела, погруженного в жидкость, совпадает с поверхностью жидкости в нашем мысленном эксперименте, следовательно, найденное выражение и есть «выталкивающая’’ сила — сила Архимеда
F Арх = -Vg. (*)
Это равенство и носит название закон Архимеда.
2. Неприменимость закона Архимеда для случая свободных тел
Казалось бы, решение задач с использованием этого закона не должно вызывать затруднений. Однако неверные решения отдельных задач на закон Архимеда встречаются не только у школьников, но и в ряде задачников.
Дело в том, что при использовании этого (как и любого другого) закона надо всегда помнить, как и для каких ситуаций он выводился. Так, например, мы вычисляли силу гидростатического давления, действующую на поверхность неподвижного объема жидко сти, находящейся в равновесии, т. е. имеющей нулевые скорость и ускорение. Следовательно, и использовать выведенное выражение для силы Архимеда можно только в тех случаях, когда и скорость, и ускорение тела равны нулю.
Покажем, что применение этого закона в других ситуациях абсолютно неправомочно, так как приводит к неверным результатам.
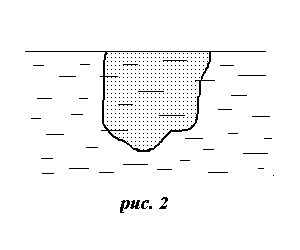
Рассмотрим легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg=
Vg и сила натяжения нити T, а вверх — сила гидростатического давления
где - плотность тела, - плотность жидкости. Условие равновесия тела
Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вве рх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения
Предположив, что в этом случае можно использовать закон Архимеда, подставим - Vg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение
Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.
Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости).
3. Сила гидростатического давления для случая свободных тел
Точный расчет гидростатического давления на поверхность ускоренно движущегося тела возможен только с применением аппарата математической физики, а ответ представим в аналитическом виде лишь для некоторых частных случаев. Уравнения, описывающие движение тела в жидкости, были впервые получены профессором Петербургского университета Леонардом Эйлером в середине XVIII века. Решение этой задачи для случая тела сферической формы, размеры которого много меньше размеро в сосуда, приведено в Приложении (для читателей, владеющих методами постановки и решения граничных задач математической физики). Полученное там выражение (**) для силы давления отличается от (*):
(4)и, с учетом (2), ускорение тела имеет вид:
(5)4. Выводы
Сравнивая выражения (4) и (*) видим, что они совпадают только при = . Зависимость силы гидростатического давления, действующей на свободное тело, от его плотности представлена на графике рис. 4 в сравнении со стандартным выражением для силы Архимеда Vg:
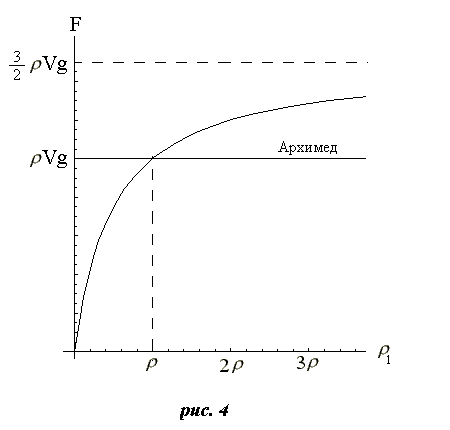
Из графика на рис.4 видно, что для малых плотностей тела сила давления убывает до нуля, а при увеличении плотности эта сила стремится к величине 1,5Vg.
На следующем графике (рис. 5) приведена зависимость ускорения свободного тела в жидкости от его плотности [уравнение (5)]. Для сравнения приведен график ускорения, получающийся непосредственн о из закона Архимеда [уравнение (3)]
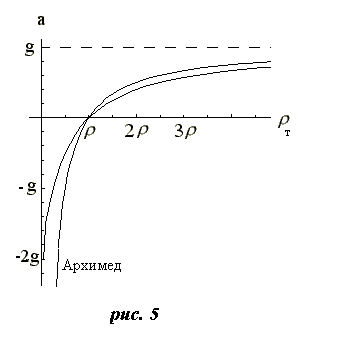
Из этого графика видно, что даже бесконечно легкий шарик всплывает с конечным ускорением, равным -2g, а тяжелые тела тонут с ускорением, меньшим, чем это следует из закона Архимеда.