Приведем вывод этих преобразований, основанный только на принципе относительности (т. е. на равноправии всех инерциальных систем отсчета).
В этом выводе постулат постоянства скорости света не используется ad hoc, а оказывается следствием принципа относительности.
Обозначим множество всех инерциальных систем отсчета K. Рассмотрим две инерциальные системы отсчета k, k' из K, движущиеся друг относительно друга со скоростью u. Выберем декартовы координаты в этих системах отсчета так, чтобы в начальный момент времени начала коор инат совпадали, а оси были параллельны.
В системе отсчета k моменты времени и координаты вдоль направления u будем обозначать t и x соответственно, в системе отсчета k' — t' и x' .
Оси X и X' направим так, чтобы система k' двигалась со скоростью u относительно системы k вдоль оси X, а система k двигалась со скоростью -u вдоль оси X' системы k' .
Равномерное движение свободной материальной точки со скоростью v в системе k описывается уравнением
а в системе k' — уравнением
Преобразование координат t, x, y, z системы k в координаты t', x', y', z' системы k' должно быть таким, чтобы уравнение (L1) переходило в уравнение (L2). Это означает, что прямая в пространстве r, t должна переходить в прямую в пространстве r', t'.
Таким свойством обладает линейное преобразование. (см. примечание 1)
| t' = att(u)t+atx(u)x+aty(u)y+atz(u)z, x' = axt(u)t+axx(u)x+axy(u)y+axz(u)z, y' = ayt(u)t+ayx(u)x+ayy(u)y+ayz(u)z, z' = azt(u)t+azx(u)x+azy(u)y+azz(u)z, |
где величины aij зависят только от скорости относительного движения систем отсчета.
При нашем выборе направления этой скорости вдоль параллельных осей X, X' общий вид линейных преобразований можно упростить:
| t' = att(u)t+atx(u)x, x' = axt(u)t+axx(u)x, y' = y, z' = y. |
(L3)
(L4)
(L5)
|
Действительно, в силу однородности и изотропности нашего пространства, преобразования вдоль оси X не должны зависеть от значения координат y и z. Сами координаты y и z тоже не должны преобразовываться, иначе поперечные размеры тел будут зависеть от скорости их движения, что приведет к неравноправию различных инерциальных систем отсчета. (см. примечание 2)
(Для тех, кого эти соображения не убедили, здесь приведен вывод преобразований Лоренца в трехмерной векторной форме)
Найдем явный вид четырех неизвестных функций att(u), atx(u), axt(u), axx(u), опираясь только на принцип относительности и с войства однородности и изотропности нашего пространства-времени.
Повернем оси координат в двух системах отсчета вокруг некоторого направления, перпендикулярного скорости u, на 1800. Это приведет замене x на -x и x' на -x '. Если теперь заменить направление скорости u на противоположное, т. е. на -u, то преобразования (L3), (L4) примут вид
| t' = att(-u)t-atx(-u)x, x' =-axt(-u)t+axx(-u)x |
(L6) (L7) |
Заметим, что произведенные преобразования привели к тому, что система k' движется, как и прежде, вдоль оси X системы k со скоростью u. В силу изотропности нашего пространства (равноправия всех направлений) вид равенств (L3), (L4) не зависит от направления осей X, X' следовательно формулы (L6), (L7) должны совпадать с (L3), (L4).
Это возможно, если функции att(u), axx(u) - четные, а функции axt(u), atx(u) — нечетные.
Теперь учтем, что точка x=0 движется со скоростью -u вдоль оси X' в системе k': x'=-ut'.
Из уравнений (L3), (L4) следует axt(u)= vuatt(u).
Аналогично точка x'=0 движется со скоростью u вдоль оси X в системе k: x=ut. Из тех же уравнений следует axt(u)= -uaxx(u) или a xx(u)= att(u)?a(u). Вводя для симметрии вместо нечетной функции atx(u) четную функцию g(u) по формуле atx(u)= -ua(u)g(u), получаем
| t' = a(u)[t-u g(u)x], x' = a(u)[x -ut]. |
(L8) (L9) |
Рассмотрим еще одну инерциальную систему отсчета k'', движущуюся со скоростью u ' вдоль о си X' системы k'. Закон преобразования из системы k' в систему k'' должен иметь вид, аналогичный (L8), (L9):
| t'' = a(u')[t'-u' g(u')x'], x'' = a(u')[x' -u't']. |
(L10) (L11) |
Подставляя в (L10), (L11) выражения для x', t' из (L8), (L9), получаем
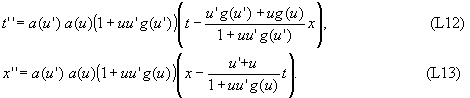
С другой стороны, равенства (L12), (L13) описывают переход из системы k в систему k' , движущуюся вдоль оси X с некоторой скоростью u'':
| t'' = a(u'')[t-u'' g(u'')x], x'' = a(u'')[x -u''t]. |
(L14) (L15) |
Из сравнения соотношений (L12), (L13) с (L14), (L15) следуют равенства
| g(u)=g(u')=g=const, | (L16) |
| a(u'')=a(u)a(u')(1+uu'g), | (L17) |
| u''=(u+u')/(1+uu'g). | (L18) |
Равенство (L16) вводит некоторую постоянную величину, размерность которой — обратный квадрат скорости. Эта величина одинакова в о всех системах отсчета, и ее численное значение не может быть выведено из каких-либо общих принципов. Экспериментальное значение этой величины g=c-2 , где c — скорость света в вакууме. В классической нерелятивистской механике g=0.
Равенство (L17) — функциональное уравнение, из которого (с учетом (L18)) можно определить вид неизвестной функции a(u) (см. примечание 3):
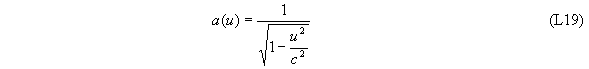
Равенство (L18) определяет закон сложения скоростей для движений вдоль оси X:
u' - скорость движения точки вдоль оси X' в системе отсчета k',
u — скорость движения системы k' вдоль оси X в системе от счета k,
u'' — скорость движения точки вдоль оси X в системе отсчета k .
Важное свойство этого закона:
если u', то u'';
если u'=c, то u''=c;
если u'>c, то u''>c.
Следовательно, если скорость частицы (или электромагнитной волны) равна c в одной системе отсчета, то она одинакова во всех инерциальных системах отсчета.
Итак, мы вывели соотношения (*) из принципа относительности и получили следствием постоянство скорости c во всех инерциальных системах отсчета. Важно отметить принципиальное отличие данного подхода к выводу преобразований Лоренца от общепринятого. Постоянство скорости света во всех инерциальных системах отсчета — это экспериментальный факт, установленный с определенной степенью точности. Приведенный выше вывод не опирается на этот факт, из него следует только существование скорости, одинаковой во всех инерциальных системах отсчета.
Из преобразований Лоренца можно получить интересные следствия.







