Общий вид линейных преобразований
| t' = att(u)t+atx(u)x+aty(u)y+atz(u)z, x' = axt(u)t+axx(u)x+axy(u)y+axz(u)z, y' = ayt(u)t+ayx(u)x+ayy(u)y+ayz(u)z, z' = azt(u)t+azx(u)x+azy(u)y+azz(u)z, |
можно записать через трехмерные вектора:
| t' = a(u)t+b(u)(ur), r'|| = d(u)ut+e(u)r||, r'^ =f(u)r^ . |
(L3d) (L4d) (L5d) |
Теперь учтем, что точка r=0 движется со скоростью -u вдоль оси X' в системе k': r'=-ut'.
Из уравнений (L3d), (L4d) следует d(u)= -a(u). Для симмтерии заменим b(u)=-a(u)g(u)
Аналогично точка r'=0 движется со скоростью u вдоль оси X в системе k: r=ut . Из тех же уравнений следуетe(u)= a(u):
| t' = a(u)[t-g(u)(ur)], r'|| = a(u)[ r|| -ut]. |
(L8d)
(L9d)
|
Рассмотрим еще одну инерциальную систему отсчета k'', движущуюся со скоростью u' вдоль оси X' системы k'. Закон преобразования из системы k' в систему k'' должен иметь вид, аналогичный (L8), (L9):
| t'' = a(u')[t'-g(u')(u'r')], r''|| = a(u')[ r'|| -u't'], r''^ =f(u')r'^ . |
(L10d) (L11d) (L11pd) |
Подставляя в (L10d), (L11d) выражения для r', t' из (L5d), (L8d), (L9d), получаем
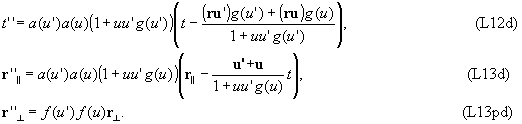
С другой стороны, равенства (L12d), (L13d), (L13pd) описывают переход из системы k в систему k', движущуюся вдоль оси X с некоторой скоростью u'':
| t'' = a(u'')[t-g(u'')(u''r)], r''|| = a(u'')[r|| -u''t], r''^ =f(u'')r^ . |
(L14d)
(L15d)
(L15pd)
|
Из сравнения соотношений (L12d), (L13d) с (L14d), (L15d) следуют равенства
| g(u)=g(u')=g=const, |
(L16d)
|
| a(u'')=a(u)a(u')(1+uu'g), |
(L17d)
|
| u''=(u+u')/(1+uu'g), |
(L18d)
|
| f(u'')=f(u)f(u'). |
(L18pd)
|
Равенства (L16d), (L17d), (L18d) совпадают с (L16), (L17), (L18), а (L18pd) с учетом (L18d) позволяет сделать вывод, что 0f(u) =1, т. е. поперечные координаты действительно не преобразуются при линейных преобразованиях Лоренца.
Окончательно в векторной форме имеем
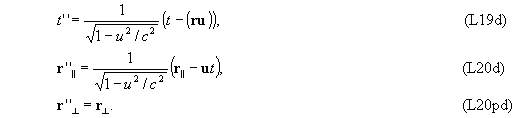
Заметим, для полноты, что в формулах (L20d), (L20pd)
r||=u(ru)/u2, r ^=r-u(ru)/u2









