Оптимальное выделение сигнала из шума можно проводить различными методами, в зависимости от того, какая ставится задача — обнаружение сигнала, сохранение формы сигнала и т.д. В каждом методе оптимальной фильтрации вводится понятие критерия оптимальности, согласно которому строится оптимальный алгоритм обработки сигнала [ 11].
Конкретный алгоритм оптимальной фильтрации будет существенно зависеть от того непериодический или периодический сигнал должен быть выделен (обнаружен) на фоне шума. По отношению к периодическому сигналу далее различаются ситуации: известна или нет его частота повторения. Ниже эти варианты задач будут рассмотрены последовательно.
Оценим возможную эффективность обнаружения непериодического сигнала при его аддитивной смеси с белым шумом. При формулировке задачи нахождения коэффициента передачи «оптимального» фильтра используются существенные требования относительно сигнала: во-первыхсчитается известной форма сигнала f(t) и соответственно его спектр 
, во вторых сигнал считается ограниченным во времени:
(3.1)
Т.е. сигнал имеет конечную длительность.
Определение оптимальности фильтра формулируется следующим образом:
Оптимальным фильтром в задаче обнаружения одиночного импульса конечной длительности является фильтр, обеспечивающий максимальное отношение пиковой мощности сигнала к мощности шума в момент окончания импульса.
Комплексный коэффициент передачи такого оптимального фильтра прямо определяется спектром заданного, подлежащего обнаружению сигнала (т.е. его формой и длительностью 
) [2 ]
Так, если сигнал имеет спектр
(3.2)и длительность его , то функция
есть функция комплексно сопряженная функции спектральной плотности сигнала.
Можно показать [2], что комплексный коэффициент передачи оптимального фильтра, в приведенном выше смысле определяется так:
или
(3.3)Не воспроизводя выкладки доказательства формулы (3.3) приведенных в ряде источников (например [ 2] ), остановимся на физическом смысле результата.
Замечая, что фазовая характеристика коэффициента передачи в (3.3) есть
видим, что 
— компенсирует фазовые сдвиги составляющих сдвиги спектра сигнала (3.2), что формирует «пик» импульса на выходе, а линейная функция — 
обеспечивает задержку этого «пика» на время длительности сигнала, т. е. этот пик приходится на момент окончания сигнала.. Можно сказать, что обеспечивается накопление полезного сигнала на интервале всего времени существования импульса.
Формула (3.3) устанавливает также, что модуль коэффициента передачи должен совпадать с модулем спектральной плотности функции заданного сигнала, т. е. оптимальный фильтр ослабляет спектральные составляющие шума тем сильнее, чем меньше модуль , В результате полная мощность шума на выходе фильтра оказывается меньшей, чем при равномерной АЧХ.
Наконец отметим, что произвольная константа 
размерна. При безразмерном 
имеет размерность обратной спектральной плотности сигнала.
Будем исходить из приведенного выше выражения (3.3). Заметим, что для сигнала (импульса) сложной формы синтез оптимального фильтра является не простой задачей. По этому искомую оценку отношения сигнал/шум проведем на примере прямоугольного импульса.
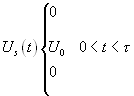(3.4)
Будем считать, что полезный сигнал представляет собой одиночный прямоугольный импульс (3.4) длительностью 
и с напряжением 
, изображенный на рис 1.
Его спектральная плотность описывается функцией
и сопряженная 
следовательно, для данного импульса в соответствии с (3.3) имеем:
(3.5).Такой коэффициент передачи может быть обеспечен схемой рис 2.
Содержащей идеальное интегрирующее звено (
), линию задержки (
) и схему вычитания .
Найдем сигнал на выходе оптимального фильтра для рассматриваемого примера (
=1)
(3.6).Таким образом, импульс на выходе имеет треугольную форму с основанием 2t и максимальным значением U0 при t=t . Оценим теперь мощность шума на выходе этого оптимального фильтра. Используем формулы (3.3) и (3.5). Положим a =1 Будем считать шум ’ белым’.
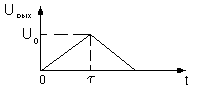
Представим модуль оптимального коэффициента передачи в виде
(3.7)
Мощность шума на выходе фильтра в соответствии с (2.2 ) и (2.3) определиться так
(3.8).
Этот табличный интеграл [3] имеет значение: 
. Таким образом, искомая величина мощности шума равна:
откуда искомое отношение мощности сигнала к мощности шума для данного оптимального фильтра будет:
(3.10).а для отношения амплитуд сигнал/шум
(3.11).В заключение еще раз отметим, что оптимальный фильтр, построенный по указанному выше критерию, жестко связан с полезным входным сигналом: изменение полезного входного сигнала ведет к необходимости изменения коэффициента передачи фильтра.
Учитывая сложность задачи синтеза оптимального фильтра , в результате которого находится его функция 
можно подойти к задаче по другому.
Сигналу выбирается тип АЧХ фильтра, сообразуясь с формой сигнала-импульса (точнее модулем его спектра). Например, для рассмотренного выше прямоугольного импульса выбирается фильтр НЧ, для импульса с высокочастотным заполнением- резонансный фильтр и т.д. Далее задача оптимизации ставится относительно выбора параметра фильтра — полосы его пропускания. Следуя этому подходу далее рассматривается возможность выделения полезного сигнала из белого шума не с помощью описанного выше оптимального фильтра, а с помощью линейного RC фильтра нижних частот. При этом полоса фильтра будет выбираться таким образом, чтобы достигнуть максимально возможного (для фильтра нижних частот) энергетического соотношения сигнал/шум к концу импульса.
Пусть полный входной сигнал U(t) выражается в виде суммы полезного входного сигнала 
и белого шума 
— случайного процесса, у которого спектральная плотность 
не зависит от частоты
(3.12).
В качестве фильтра нижних частот будем рассматривать интегрирующую цепочку (рис 4) — низкочастотный фильтр первого порядка с постоянной времени 
и коэффициентом передачи
(3.13).
При исследовании прохождения шума через линейную систему будем использовать формулу (2.3) ,квадрат модуля коэффициента передачи
(3.14).где 
— полоса пропускания рассматриваемого фильтра нижних частот по уровню 0.707. Требуется найти полосу 
заданного фильтра нижних частот, обеспечивающую максимальное отношение сигнал/шум на выходе фильтра.
Можно рассматривать прохождение через фильтр нижних частот полезного сигнала и шума раздельно, так как интегрирующая цепочка — линейная схема.
Сигнал на выходе линейной системы может быть найден с помощью спектрального метода.
(3.15).где коэффициент передачи интегрирующей цепочки определяется формулой (3.14) , а спектральная плотность полезного входного сигнала (3.4) была найдена как интеграл Фурье
(3.16).Подставив в (3.15) формулы (3.16) и (3.13) и вычислив интеграл, получаем следующее выражение для сигнала на выходе фильтра
при
(3.17)
Таким образом, выходной сигнал достигает своего максимального значения в момент окончания входного импульса t=t
(3.18).Это выражение зависит от соотношения полосы частот фильтра 
(3.13) и полосы частот, занимаемой полезным сигналом 
, которая связана с длительностью прямоугольного импульса так 
1/t . С учетом этого выражение (3.18) можно преобразовать следующим образом
(3.19).Если полоса частот, занимаемая спектральной плотностью полезного входного сигнала, меньше полосы частот, определяемой коэффициентом передачи интегрирующей цепочки 
, то максимальное значение полезного сигнала на выходе интегрирующей цепочки (3.18) равно 
и не зависит от полосы фильтра при 
.
Если же полоса частот, занимаемая спектральной плотностью полезного входного сигнала, больше полосы частот, занимаемой коэффициентом передачи интегрирующей цепочки, 
, то разложив экспоненту в выражении (3.18) в ряд, получаем следующее максимальное значение полезного сигнала на выходе интегрирующей цепочки
В этом случае амплитуда полезного сигнала на выходе фильтра линейно зависит от полосы фильтра 
.
Мощность полезного входного сигнала, входящая в энергетическое отношение сигнал/шум, будет пропорциональна, таким образом, квадрату от полосы фильтра
Следовательно, если полоса фильтра перекрывает полосу полезного входного сигнала, то дальнейшее увеличение полосы фильтра не приводит к увеличению полезного выходного сигнала. Если же полоса фильтра уже полосы сигнала, то увеличение полосы фильтра приводит к увеличению мощности полезного выходного сигнала, пропорционально квадрату полосы фильтра.
Для мощности шума на выходе фильтра с помощью формул (2.2) и (2.3) может быть получено следующее выражение
(3.20),в котором положим 
— спектральная плотность мощности белого шума, а квадрат модуля коэффициента передачи определен формулой (3.14). Вычислив интеграл , получаем
(3.21),где 
— ширина полосы фильтра по уровню 1/
.
Отсюда следует, что мощность шума на выходе фильтра линейно зависит от полосы коэффициента передачи интегрирующей цепочки.
Используя полученные выражения для максимального значения выходного полезного сигнала (3.18) и мощности шума на выходе фильтра (3.21), можно получить выражение для энергетического отношения сигнал/шум на выходе фильтра нижних частот (RC-цепочки):
(3.22),где
и 
(3.23)Искомую величину оптимальной полосы 
для выбранного НЧ фильтра (3.13) и сигнала (3.4), обеспечивающей максимальное отношение сигнал/шум в момент t=t , найдем из условия максимума функции (3.23), т.е .
(3.24).Функция 
имеет пологий максимум, ее график приведен на рис 6. 
Таким образом
И следовательно отношение пиковой мощности сигнала и мощности шума при оптимальной полосе НЧ фильтра равно
(3.25).Отношение же амплитуды сигнала к «амплитуде» шума будет
(3.26).Напомним, что использование фильтра с оптимальным коэффициентом передачи(3.5) приводило к отношению сигнал/шум по мощности равному (3.10)
(3.10).Сравнивая (3.10) с (3.25), видим, что использование RC фильтра НЧ (3.13) с правильно выбранной полосой вместо фильтра с оптимальным коэффициентом передачи приводит к ухудшению соотношения сигнал/шум по мощности на 19 %.
(3.27),и лишь на 10% по отношению амплитуд сигнал/шум
(3.28).Т.о. для конкретного сигнала — прямоугольного импульса использование простого RC фильтра НЧ можно считать оправданным (целесообразным).
Качественно такой результат понятен. Если полоса фильтра уже полосы сигнала, то целесообразно увеличивать полосу фильтра, так как при этом мощность полезного сигнала на выходе растет пропорционально квадрату полосы, а мощность шума растет пропорционально первой степени полосы. Если полоса фильтра шире полосы сигнала, то целесообразно уменьшать полосу фильтра, так как при этом мощность полезного сигнала на выходе не меняется, а мощность шума уменьшается пропорционально первой степени полосы.
Далее найдем соотношение сигнал/шум для многозвенного RC — фильтра низкой частоты.
Рассмотрим теперь задачу определения оптимальной полосы многозвенного фильтра с целью обеспечения максимального отношения сигнал/шум в момент окончания импульса. Импульс будем, как и раньше, считать прямоугольным.(3.4). Конкретно рассмотрим фильтр, собранный идентичных RC — звеньев, разделенных буферными каскадами.(рис 7).
Коэффициент передачи такого фильтра описывается функцией
(3.29)
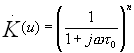
Если зафиксировать полосу пропускания этого фильтра 
на заданном уровне неравномерности 
, то эти два параметра, как это следует из (3.29), оказываются связанными уравнением
(3.30).Отсюда очевидно, что для обеспечения постоянства общей заданной полосы фильтра при изменении числа звеньев n, постоянную 
необходимо изменить следующим образом
(3.31).При увеличении числа звеньев n, будет увеличиваться крутизна спада АЧХ в области частот, выше заданной полосы 
. (рис 8).
Переходная характеристика h(t) для рассматриваемого фильтра (3.29) — реакция на включение ступеньки напряжения на входе определяется так:
(3.32).
где 
, как отмечено выше, если при увеличении числа каскадов n ставится требование 
=const ( на заданном уровне неравномерности 
), то параметр 
каждого каскада должен изменятся в соответствии с формулой (3.31). Пример зависимости 
от n для n=1 и n=5 при одинаковой приведен на рис.8, а зависимость переходной характеристики h(t) также при n=1 и n=5 приведен на рис.9.
Оценим теперь уровень шума на выходе фильтра. Считаем шум на выходе белым, имеющим спектральную плотность мощности S0
(3.33).Значение этого табличного неопределенного интеграла (3.36) известно [ 3].
(3.34).При вычислении определенного интеграла (3.34) следует учесть, что функция 
равна нулю на верхнем (
) и на нижнем (-) пределах. Поэтому
(3.35).Учитывая также необходимое изменение RC каждого каскада фильтра при увеличении n (при требовании =const) получаем интересующий количественный результат. В качестве примера приводим численные данные расчета мощности шума и напряжения шума для фильтров разных порядков (n).
и 
(3.36).
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0.707 |
0.78 |
0.85 |
0.9 |
0.95 |
1.01 |
|
|
0.5 |
0.61 |
0.72 |
0.81 |
0.91 |
1.025 |
Полученные выше данные о прохождении импульсного сигнала и белого шума через n-звенныйфильтр низкой частоты позволит определить оптимальную полосу фильтра ( при заданной длительности импульса) и соотношение сигнал/шум на выходе рассматриваемого фильтра в момент окончания импульс t=t при оптимальном выборе его полосы 
. Как и в случае однозвенного фильтра строим функцию отношения величины полученного сигнала к «амплитуде» шума
(3.37).Здесь 
, 
-коэффициент изменения RC=
каждого звена, при изменении порядка фильтра n (3.31)
Отношение 
, как функция 
,имеет пологий max, зависящий от порядка фильтра n.
Так, например, для трехзвенного фильтра max 
достигается при 
, и значении 
. Для пятизвенного фильтра получаем 
и 
. Из этих значений определяется оптимальная величина параметра фильтра 
.
Т.о. искомое отношение амплитуд сигнал/шум с учетом коэффициентов Ki в соответствии с выражением (3.37) дает:
(3.38),
(3.39).Сравнивая эти результаты с полученными ранее, видим, что повышение порядка фильтра дает худшее отношение сигнал/шум, чем для фильтра первого порядка (3.13):
и 
(3.40).Поэтому, если «оптимальный» фильтр определяемый требованием 
(см(3.3)) заменяется фильтром RC с оптимально подбираемым параметром, то в рассматриваемом случае прямоугольного импульса лучшим оказывается простейший RC фильтр первого порядка .
Этому предпочтению можно дать следующие объяснения.
Во-первых, АЧХ RC фильтр первого порядка оказывается ближе к модулю спектра прямоугольного импульса, чем АЧХ фильтров более высоких порядков. Напомним, что для «оптимального» фильтра в соответствии с (3.3) оказывается, что его АЧХ совпадает с модулем спектра сигнала.
Во-вторых, как показано выше, значение обобщенного параметра 
, обеспечивающего наибольшее отношение мощности сигнала к мощности шума в конце импульса, увеличивается с повышением порядка фильтра. Так например, при n=1 значение 
, при n=3 имеем, что 
, а при n=5 обобщённый параметр 
.
Поэтому при заданной длительности импульса t полоса фильтра 
, требуется большей, для фильтра более высокого порядка, что также приводит к повышению шума.
Физически последнюю зависимость от n можно объяснить ростом группового запаздывания, т. е. требуемое максимальное отношение
к концу импульса достигается для больших n при больших значениях 
. Что при фиксированной длительности импульса означает большее значение 
. А это , естественно, увеличивает шум на выходе фильтра.