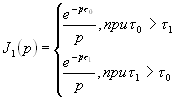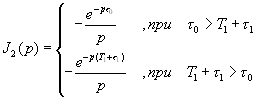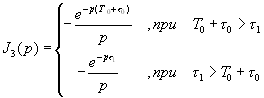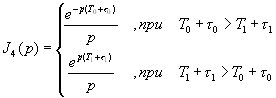В случае периодического сигнала целесообразно использовать его накопление в течении ряда периодов. Покажем, как может быть получен существенный выигрыш в отношении сигнал/шум на выходе фильтра. На периодическом сигнале этот выигрыш может быть реализован в статических свойствах сигнала и шума (который по прежнему будем считать«белым»). В частности, может быть использовано различие в корреляционных функциях детерминированного сигнала и шума. При этом мы рассмотрим последовательно два варианта построения «корреляционных фильтров». В первом — будем считать, что сигнал периодический, но период не известен;во-втором — период сигнала известен, но не известна его «фаза».
Рассмотрим первый вариант.
Используем алгоритм оценки корреляционной функции
Здесь ![]() и
и ![]() автокорреляционные функции сигнала и шума, а
автокорреляционные функции сигнала и шума, а ![]() и
и ![]() — взаимокорреляционные функции сигнала и шума. Так как сигнал и шум можно считать не зависимыми процессами, то взаимно корреляционные функции
— взаимокорреляционные функции сигнала и шума. Так как сигнал и шум можно считать не зависимыми процессами, то взаимно корреляционные функции ![]() и
и ![]() равны нулю.
равны нулю.
Оценим теперь ![]() и .
и . ![]() Будем считать, что на входе корреляционного фильтра включен аналоговый НЧ фильтр первого порядка (3.14). Тогда, в соответствии с (2.1), имеем
Будем считать, что на входе корреляционного фильтра включен аналоговый НЧ фильтр первого порядка (3.14). Тогда, в соответствии с (2.1), имеем
При вычислении интеграла будем различать два случая: ![]() и
и ![]() . Напомним, что
. Напомним, что ![]() — задержка выборочных значений (сдвиг аргумента) второго сомножителя в подынтегральной функции (4.1). Знаменатель подынтегральной функции имеет два корня:
— задержка выборочных значений (сдвиг аргумента) второго сомножителя в подынтегральной функции (4.1). Знаменатель подынтегральной функции имеет два корня: ![]() .
.
Вычисляя этот интеграл по формуле разложения [4,5], по вычетам, получаем с учетом знания ![]() , явный вид:
, явный вид:
Полагая ![]() , получаем мощность шума на выходе:
, получаем мощность шума на выходе:
Напомним, что этот результат был получен и ранее ,формула (3.22).
Значение функции корреляции для периодического сигнала было приведено выше (1.14). Учитывая его, получаем значение искомой корреляционной функции:
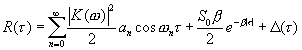 (4.5)
(4.5)Член![]() имеет смысл «шума», обусловлен величиной суммы
имеет смысл «шума», обусловлен величиной суммы ![]() при конечном времени интегрирования и усреднения ,стремится к нулю при увеличении T и t. Обращаясь к (4.5) видим, что при увеличении сдвига-задержки
при конечном времени интегрирования и усреднения ,стремится к нулю при увеличении T и t. Обращаясь к (4.5) видим, что при увеличении сдвига-задержки ![]() первое слагаемое (сумма) описывает неубывающую осциллирующую функцию, полезный сигнал по аргументу
первое слагаемое (сумма) описывает неубывающую осциллирующую функцию, полезный сигнал по аргументу ![]() ( а не t) , второе — экспоненциально убывает. Таким образом обеспечивается принципиальная возможность выделить осциллирующий член — полезный сигнал из аддитивной смеси сигнала и шума, имеющейся на входе фильтра. Следует обратить внимание, что для реализации рассмотренного способа необходимо на каждом шаге изменения
( а не t) , второе — экспоненциально убывает. Таким образом обеспечивается принципиальная возможность выделить осциллирующий член — полезный сигнал из аддитивной смеси сигнала и шума, имеющейся на входе фильтра. Следует обратить внимание, что для реализации рассмотренного способа необходимо на каждом шаге изменения ![]() вычислять соответствующие интегралы по интервалу Т, чтобы обеспечить малую величину приближенных величин взаимокорреляционных функций
вычислять соответствующие интегралы по интервалу Т, чтобы обеспечить малую величину приближенных величин взаимокорреляционных функций ![]() и
и ![]() . (см. рис. 10)
. (см. рис. 10)
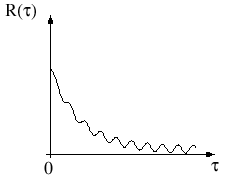
Рис. 10
Конечная величина интервала интегрирования приводит к тому, что величина D (t) 0 будет «шумом».Величину такого рода «шума» достаточно просто оценить для случая, когда период полезного сигнала известен.
Рассмотрим теперь случай, когда период полезного сигнала известен, но неизвестна его «фаза», да и само наличие под вопросом. В этом варианте целесообразно использовать алгоритм вычисления взаимокорреляционной функции аддитивной смеси полезного сигнала и шума и опорным сигналом , период которого равен периоду полезного сигнала. Возможный выигрыш в отношении сигнал/шум рассмотрим на примере гармонического сигнала. Опорный сигнал тоже положим гармоническим, но с другой амплитудой и фазой. Шум будем считать «белым».
Таким образом искомая взаимокорреляционная функция будет
Второй член в (4.8) можно рассматривать, как фон при конечном времени интегрирования, тогда, как третий интеграл имеет смысл «шума».
И «фон» и «шум» убывают при увеличении времени интегрирования Т. Очевидно, что «фон» убывает как 1/Т. Характер убывания «шума» при увеличении Т рассмотрим более подробно, отдельно.
Для оценки величины «шума» используем соотношение Хинчина [12]:
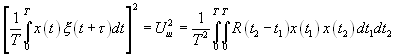 (4.9).
(4.9).Здесь ![]() — корреляционная функция случайного процесса, x(t)- детерминированная функция. Примем условия рассмотренного выше примера: шум на входе будем полагать «белым» со спектральной плотностью мощности
— корреляционная функция случайного процесса, x(t)- детерминированная функция. Примем условия рассмотренного выше примера: шум на входе будем полагать «белым» со спектральной плотностью мощности ![]() , на входе корреляционного фильтра включен RC фильтр с коэффициентом передачи.
, на входе корреляционного фильтра включен RC фильтр с коэффициентом передачи.
Выше было показано, что корреляционная функция случайного процесса на выходе такого RC фильтре имеет вид:
Подставляя эти функции в (4.9) и вычисляя двойной интеграл, получаем громоздкое выражение ( см.приложение), включающее члены, имеющие различное убывание при увеличении интервала интегрирования Т.
Если учесть только наиболее медленно убывающий член 1/T, то приближенно получаем:
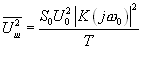 (4.10).
(4.10).Эта формула и описывает мощность «шума» на выходе корреляционного фильтра, обусловленного конечным временем интегрирования Т. «Амплитуда шума» соответственно:
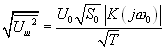 (4.11).
(4.11).Заметим, что роль частотного интервала здесь играет величина 1/T Величина же ![]() просто безрамерный коэффициент.
просто безрамерный коэффициент.
Обращаясь к (4.8), напомним, что первый член описывает взаимокорреляционную функцию детерминированных сигналов, полезного ![]() и опорного
и опорного![]() и, следовательно, имеет смысл полезного сигнала на выходе корреляционного фильтра:
и, следовательно, имеет смысл полезного сигнала на выходе корреляционного фильтра:
Очевидно, что отношение сигнал/шум, (предполагая , что ![]() выбирается так,чтобы
выбирается так,чтобы ![]() ), будет:
), будет:
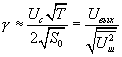 (4.13).
(4.13).Это важный результат: при накоплении периодического сигнала, которое можно вести на протяжении ряда периодов, отношение амплитуд сигнал/шум на выходе корреляционного фильтра увеличивается пропорционально корню квадратному от времени интегрирования. (![]() ). Понятно, что полученная зависимость сигнал/шум от времени интегрирования (как
). Понятно, что полученная зависимость сигнал/шум от времени интегрирования (как ![]() ) сохранится и в случае сложного периодического ( импульсного) сигнала. Заметим, что в этом случае и опорный сигнал должен иметь спектр такой же, как и спектр полезного сигнала.
) сохранится и в случае сложного периодического ( импульсного) сигнала. Заметим, что в этом случае и опорный сигнал должен иметь спектр такой же, как и спектр полезного сигнала.
Реализовать описанный алгоритм возможно используя преобразование суммарного входного сигнала в цифровую форму , что позволит далее производить все операции вычисления![]() с помощью программ на ЭВМ. При необходимости иметь выходной сигнал в аналоговой форме нужно использовать цифроаналоговый преобразователь. Кроме того, для ограничения спектра шума по входу необходимо сохранить, аналоговый фильтр, подобный рассмотренному в данном примере
с помощью программ на ЭВМ. При необходимости иметь выходной сигнал в аналоговой форме нужно использовать цифроаналоговый преобразователь. Кроме того, для ограничения спектра шума по входу необходимо сохранить, аналоговый фильтр, подобный рассмотренному в данном примере ![]() .
.
В заключение этого раздела отметим, что результат здесь был получен на «временном языке», т. е. отношение сигнал/шум на выходе корреляционного фильтра, выражено как функция времени накопления (интегрирования). Но при этом пока неочевидно каков будет коэффициент передачи корреляционного фильтра в частотной области.
Ответ на этот вопрос удобно получить, рассмотрев аналоговый вариант корреляционного фильтра.
В радиотехнических терминах такой корреляционный фильтр реализуется схемой фазового детектора. Действительно, функционально схема фазового детектора реализует алгоритм определения взаимной корреляционной функции.
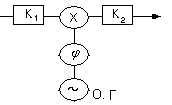
Эта схема содержит входной фильтр ![]() , генератор опорного сигнала, перемножитель входного сигнала с опорным и накопитель- инерционный узкополосный фильтр
, генератор опорного сигнала, перемножитель входного сигнала с опорным и накопитель- инерционный узкополосный фильтр ![]() , выполняющий приближенно операцию интегрирования.
, выполняющий приближенно операцию интегрирования.
Рассмотрим функционирование этой схемы, обращая внимание на преобразование спектра принимаемого (входного) сигнала.
Полезный сигнал опять будем считать гармоническим, а входной сигнал аддитивной смесью этого сигнала с «белым» шумом![]() .
.
Пусть ![]() есть резонансный RLC фильтр
есть резонансный RLC фильтр
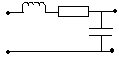
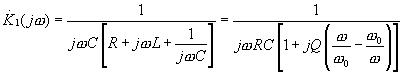 (4.14)
(4.14)будем считать ![]() узкополосным, тогда при выполнении условия
узкополосным, тогда при выполнении условия ![]() получим приближенное выражение:
получим приближенное выражение:
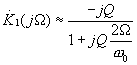 ,
, 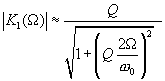 (4.15)
(4.15)Удобно ввести ширину полосы пропускания фильтра ![]() при заданной неравномерности
при заданной неравномерности ![]() , примем
, примем ![]() . Тогда
. Тогда ![]() ,
, ![]() -добротность, следовательно,
-добротность, следовательно,
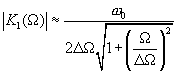 (4.16)
(4.16)Заметим, что на резонансной частоте ![]() имеем
имеем ![]() и
и ![]()
Будем далее учитывать нормированный модуль коэффициента передачи входного фильтра
Рассмотрим прохождение белого шума через такой резонансный фильтр ![]() , считая, что его спектральная плотность мощности-
, считая, что его спектральная плотность мощности-![]() .
.
Используя (2.3) , имеем выражение для спектральной плотности мощности шума на выходе резонансного фильтра ![]() , на входе перемножителя.
, на входе перемножителя.
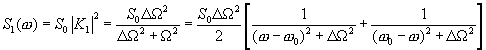 (4.18)
(4.18)В качестве второго сомножителя на перемножитель подается гармонический сигнал. Здесь возможны два варианта: первый — частота опорного сигнала равна частоте полезного сигнала (![]() ). В этом случае фильтр
). В этом случае фильтр![]() должен быть фильтром НЧ. Полезный выходной сигнал будет представлен постоянной составляющей. Второй вариант- частота опорного сигнала
должен быть фильтром НЧ. Полезный выходной сигнал будет представлен постоянной составляющей. Второй вариант- частота опорного сигнала ![]() . Здесь выходной фильтр
. Здесь выходной фильтр ![]() должен быть резонансным на частоте
должен быть резонансным на частоте ![]() .
.
Рассмотрим первый вариант:![]() , опорный гармонический сигнал
, опорный гармонический сигнал
Его спектр
Убедимся, что спектр (4.20) связан преобразованием Фурье с (4.19)
Здесь использовано известное свойство d (x) функции :![]() .
.
Итак, имеем спектры сомножителей, хотим найти спектр произведения — спектр на входе перемножителя. Используем формулу свертки в частотной области [8 ]:
Спектры сомножителей (4.19) и (4.20) изображены на рис.13
Подставив значения спектральных функций (4.18) и (4.20) в (4.22) , получим спектральную плотность мощности шума на выходе перемножителя:
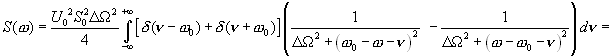
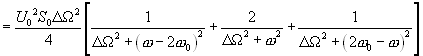 (4.23)
(4.23)Наконец, спектральная плотность мощности шума на выходе узкополосного НЧ фильтра ![]() будет содержать только полосу спектра вблизи
будет содержать только полосу спектра вблизи ![]() . Это дает:
. Это дает:
Теперь легко найти мощность шума, имеющую такой спектр. Это удобно сделать так:
найти автокорреляционную функцию, соответствующую этому спектру и устремить t -> 0
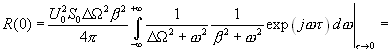
Полоса фильтра ![]() выбирается много меньше, чем у фильтра
выбирается много меньше, чем у фильтра ![]() , то есть
, то есть![]() , при этом (4.25) приблизительно дает:
, при этом (4.25) приблизительно дает:
Таким образом, мощность шума на выходе фазового детектора -корреляционного фильтра пропорциональна узкой полосе выходного фильтра![]() равной DW
равной DW![]() Аналогично оценим величину и мощность полезного сигнала. Функция взаимной корреляции полезного гармонического сигнала была определена ранее (4.8),(4.12). Она описывает величину выходного полезного сигнала, в данном случае величину постоянной составляющей как функции задержки опорного сигнала
Аналогично оценим величину и мощность полезного сигнала. Функция взаимной корреляции полезного гармонического сигнала была определена ранее (4.8),(4.12). Она описывает величину выходного полезного сигнала, в данном случае величину постоянной составляющей как функции задержки опорного сигнала ![]() .
.
Максимум сигнала на выходе фазового детектора получается при значениях
где n- целое число. Следует обратить внимание, что формула (4.12) описывает не мощность сигнала ![]() , а его величину («амплитуду»). Множителю
, а его величину («амплитуду»). Множителю ![]() следует придать смысл коэффициента усиления. Этот множитель присутствует и в выражении, оценивающем мощность шума. (
следует придать смысл коэффициента усиления. Этот множитель присутствует и в выражении, оценивающем мощность шума. (![]() ). Поэтому мощность сигнала ( его максимального значения при
). Поэтому мощность сигнала ( его максимального значения при![]() ) будет описываться так
) будет описываться так
А отношение сигнал/шум по мощности (см 4.26) есть:
соответственно, отношения сигнал/шум по амплитуде на выходе корреляционного фильтра — фазового детектора будет
Коротко рассмотрим отмеченный выше второй вариант: частота опорного генератора отлична от частоты полезного сигнала ![]() здесь после перемножения полезного сигнала с опорным получим сумму двух гармонических сигналов на суммарной и разностной частотах
здесь после перемножения полезного сигнала с опорным получим сумму двух гармонических сигналов на суммарной и разностной частотах
![]() -фаза опорного сигнала. Здесь сомножителями участвовали сигналы:
-фаза опорного сигнала. Здесь сомножителями участвовали сигналы:
В качестве узкополосного интегрирующего фильтра в этом случае нужно использовать резонансный фильтр — ( усилитель), настроенный на суммарную![]() или разностною
или разностною ![]() частоту. Отличием от рассмотренного выше варианта является то , что при изменении фазы опорного сигнала относительно фазы входного (полезного) сигнала амплитуда гармонического сигнала на разностной и суммарной частоте будет оставаться постоянной. Изменяться будет только фаза сигнала на этих частотах. Функционально схема, изображенная на рис.11 ., включающая . в качестве фильтра К2 резонансный фильтр, настроенный на
частоту. Отличием от рассмотренного выше варианта является то , что при изменении фазы опорного сигнала относительно фазы входного (полезного) сигнала амплитуда гармонического сигнала на разностной и суммарной частоте будет оставаться постоянной. Изменяться будет только фаза сигнала на этих частотах. Функционально схема, изображенная на рис.11 ., включающая . в качестве фильтра К2 резонансный фильтр, настроенный на ![]() , является типовой схемой супергетеродинного приёмника в высокочастотной её части и работает как аналоговый корреляционный фильтр. Преобразование шума в этом варианте фильтра легко оценить совершенно также, как это было сделано выше, только размещение полос спектра шума по диапазону будет другим.
, является типовой схемой супергетеродинного приёмника в высокочастотной её части и работает как аналоговый корреляционный фильтр. Преобразование шума в этом варианте фильтра легко оценить совершенно также, как это было сделано выше, только размещение полос спектра шума по диапазону будет другим.
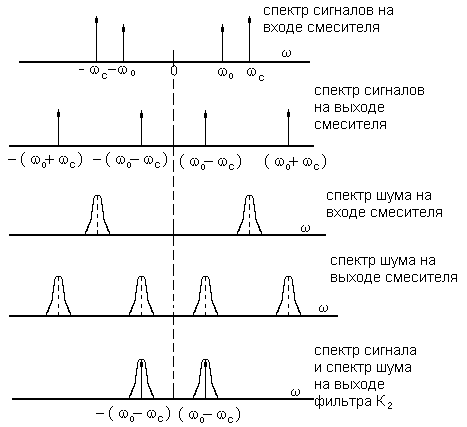
Не повторяя очевидных выкладок качественно поясним это рисунком (Рис.14), на котором по осям частот указаны частоты сигналов и полосы спектра шума. Соотношение сигнал/шум и в этом случае будут также определятся выражениями (4.28) и (4.29):
Формула (4.28) дает ответ и на вопрос об оптимальном комплексном коэффициенте передачи корреляционного фильтра. Для гармонического сигнала — это коэффициент ![]() , описывающий узкополосный выходной (интегрирующий) фильтр. В случае, когда частота опорного сигнала совпадает с частотой полезного это будет низкочастотный фильтр.(3.16) или (3.32). Если частота опорного отлична от частоты сигнала — это будет резонансный фильтр(4.15), настроенный на суммарную или разностную частоту
, описывающий узкополосный выходной (интегрирующий) фильтр. В случае, когда частота опорного сигнала совпадает с частотой полезного это будет низкочастотный фильтр.(3.16) или (3.32). Если частота опорного отлична от частоты сигнала — это будет резонансный фильтр(4.15), настроенный на суммарную или разностную частоту ![]() . В этом случае целесообразно совместить функцию фильтрации с усилением, т.е. в качестве интегрирующего элемента использовать резонансный усилитель. Однако на отношение сигнал/шум величина этого усиления влиять не будет: и шум и сигнал усиливаются одинаково.
. В этом случае целесообразно совместить функцию фильтрации с усилением, т.е. в качестве интегрирующего элемента использовать резонансный усилитель. Однако на отношение сигнал/шум величина этого усиления влиять не будет: и шум и сигнал усиливаются одинаково.
Отметим, что рассмотренные выше примеры, когда в качестве полезного сигнала рассматривается неограниченный во времени гармонический сигнал не представляет непосредственного интереса: здесь время накопления формально может стремиться к бесконечности, а полоса пропускания фильтра к нулю. (Время установления сигнала в таком фильтре будет стремиться к бесконечности).
Однако полученные результаты являются основой для оценки отношения сигнал/шум при ограниченном времени интегрирования или конечной полосе фильтра. Уместно напомнить, что полоса фильтра ![]() и время установления
и время установления ![]() связаны соотношением :
связаны соотношением : ![]() .
.
Так, например, задавшись временем наблюдения, ( можно приравнять его времени установления в наиболее узкополосном звене), получаем необходимую ширину полосы узкополосного фильтра (![]() ). А при заданных величинах входного сигнала
). А при заданных величинах входного сигнала ![]() и спектральной плотности мощности шума
и спектральной плотности мощности шума ![]() , определяем и отношение сигнал/шум на выходе. Наоборот, задавшись желаемым соотношением сигнал/шум на выходе ( при известных данных входных
, определяем и отношение сигнал/шум на выходе. Наоборот, задавшись желаемым соотношением сигнал/шум на выходе ( при известных данных входных ![]() и
и ![]() ), получаем величину требуемого времени установления (наблюдения) или полосу интегрирующего узкополосного фильтра. Оценка отношения сигнал / шум будет продолжена при рассмотрении конкретной схемы оптимального фильтра в разделе 4.5.2
), получаем величину требуемого времени установления (наблюдения) или полосу интегрирующего узкополосного фильтра. Оценка отношения сигнал / шум будет продолжена при рассмотрении конкретной схемы оптимального фильтра в разделе 4.5.2
Гораздо более интересным является случай, когда полезный сигнал является сложным периодическим сигналом. Для такого сигнала будут рассмотрены два вопроса:
-
Какой вид будет иметь взаимно-корреляционная функция, как функция временного сдвига опорного сигнала относительно входного, полезного?
-
Какова будет АЧХ оптимального фильтра для сложного (импульсного) периодического сигнала и как будет зависеть отношение сигнал/шум от параметров фильтра?
Получив ответы на эти вопросы, окажется возможным оценить выигрыш в отношении сигнал/шум при ограниченном времени наблюдения. Например, при приеме 'пачки' из n импульсов на заданном временном интервале.
Отдельно надо будет оценить необходимую разрядность аналого-цифрового преобразователя, способного реализовать требуемый выигрыш в отношении сигнал/шум.
В качестве первого примера рассмотрим выделение полезного сигнала ![]() , представляющего периодическую последовательность прямоугольных импульсов, которая принимается на фоне шума
, представляющего периодическую последовательность прямоугольных импульсов, которая принимается на фоне шума ![]() .
.
В роли приемного устройства, обеспечивающего желаемый выигрыш в отношении сигнал/шум, будем использовать корреляционный аналоговый фильтр, описанный выше. В качестве опорного сигнала будет использоваться аналогичная периодическая последовательность прямоугольных импульсов с той же частотой повторения, но, возможно другой длительности. Работу перемножителя в данном случае можно представлять как действие ключа: во время опорного импульса ключ замкнут, в его отсутствии — разомкнут. Коэффициент передачи перемножающего устройства периодически изменяется от единицы до нуля.
Для нахождения ![]() , как и ранее, используем соотношение Фурье (2.1), найдя сначала соответствующую спектральную функцию
, как и ранее, используем соотношение Фурье (2.1), найдя сначала соответствующую спектральную функцию ![]() . Для этого можно вначале определить спектр произведения одиночных импульсов, а затем, используя известную связь спектра одиночного и периодического сигналов, найти искомый спектр произведения периодических сигналов.
. Для этого можно вначале определить спектр произведения одиночных импульсов, а затем, используя известную связь спектра одиночного и периодического сигналов, найти искомый спектр произведения периодических сигналов.
Принятые обозначения параметров импульсов изображены на рисунке
Изображения этих одиночных импульсов будут соответственно
Изображение произведения временных функций определим, используя формулу свертки в частной области
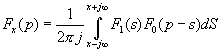 (4.32)
(4.32)Заметим, что при интегрировании (4.32) точку Х на вещественной оси и комплексную точку Р следует взять настолько далеко вправо, чтобы для точки S, перемещающейся по прямой интегрирования (от ![]() до
до ![]() ) соблюдались два условия: во-первых, чтобы S оставалось в полуплоскости сходимости изображения
) соблюдались два условия: во-первых, чтобы S оставалось в полуплоскости сходимости изображения ![]() , и во-вторых, чтобы P-S оставалось в полуплоскости изображения
, и во-вторых, чтобы P-S оставалось в полуплоскости изображения ![]() [ Дёч ]
[ Дёч ]
Подставляя (4.31) в (4.32) получаем, что необходимо вычислить четыре интеграла
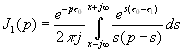 ,
, 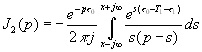
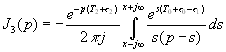 ,
, 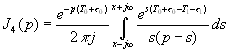 (4.33)
(4.33)Значения этих интегралов зависят от знака показателя экспоненты. Покажем, как он влияет на примере вычисления ![]() , используя формулу разложения [ ], [ ], т. е. считая его по вычетам. Знаменатель в (4.33) имеет два корня S=0 и S=P , второй корень следует считать расположенным правее исходного контура интегрирования, (в правой полуплоскости S). При
, используя формулу разложения [ ], [ ], т. е. считая его по вычетам. Знаменатель в (4.33) имеет два корня S=0 и S=P , второй корень следует считать расположенным правее исходного контура интегрирования, (в правой полуплоскости S). При ![]() , в соответствии с леммой Жордана, можем исходный контур замкнуть полуокружностью бесконечно большого радиуса в левой полуплоскости S. При этом в образовавшемся замкнутом контуре
, в соответствии с леммой Жордана, можем исходный контур замкнуть полуокружностью бесконечно большого радиуса в левой полуплоскости S. При этом в образовавшемся замкнутом контуре ![]() окажется только полюс в точке S=0. Что дает:
окажется только полюс в точке S=0. Что дает:
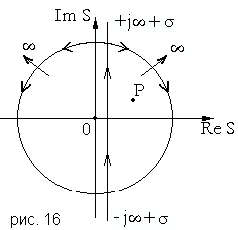
Если же ![]() , то лемма Жордана позволяет замкнуть исходный контур полуокружностью в правой полуплоскости S, теперь в замкнутом контуре окажется полюс S=P. Вычисляя этот вычет (с учетом знака (-)из-за изменения направления обхода по замкнутому контуру L), получаем:
, то лемма Жордана позволяет замкнуть исходный контур полуокружностью в правой полуплоскости S, теперь в замкнутом контуре окажется полюс S=P. Вычисляя этот вычет (с учетом знака (-)из-за изменения направления обхода по замкнутому контуру L), получаем:
Аналогично вычисляются и остальные интегралы (![]() ,
,![]()
![]() и
и ![]() ).
).
Результаты вычисления представлены в таблице 1.
|
Таблица 1 |
(4.34)
|
|
|
|
|
|
|
Очевидно, что искомое изображение ![]() (4.32) на выходе перемножителя-ключа получается суммированием
(4.32) на выходе перемножителя-ключа получается суммированием ![]() с учетом взаимного положения
с учетом взаимного положения ![]() и
и ![]() во времени. Наглядно этот результат представлен на рисунке (в случаях B,C,D,E не выписаны сокращающиеся слагаемые).
во времени. Наглядно этот результат представлен на рисунке (в случаях B,C,D,E не выписаны сокращающиеся слагаемые).
Приведенные данные позволяют построить и функцию взаимной корреляции на выходе узкополосного, интегрирующего звена ![]() , выделяющего (в данном примере) постоянную составляющую, величина которой зависит от взаимного положения импульсов во времени. Учитывая, что при изменении сдвига-задержки
, выделяющего (в данном примере) постоянную составляющую, величина которой зависит от взаимного положения импульсов во времени. Учитывая, что при изменении сдвига-задержки ![]() опорного сигнала на входе звена
опорного сигнала на входе звена ![]() меняется длительность импульса
меняется длительность импульса ![]() и учитывая, что постоянная составляющая в спектре пропорциональна
и учитывая, что постоянная составляющая в спектре пропорциональна ![]() , имеем:
, имеем:
 (4.35)
(4.35)
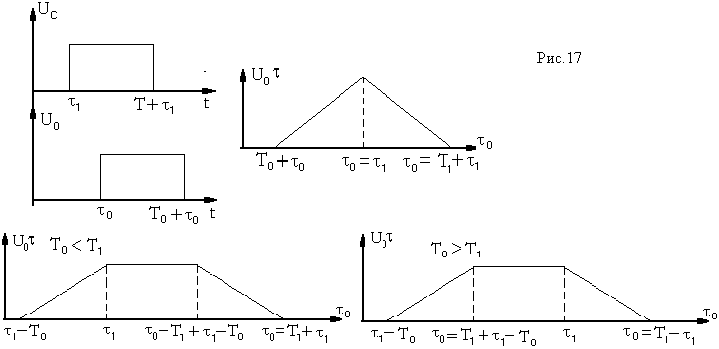
Получаем, что при изменении временного положения опорного импульса относительно сигнала ![]() взаимокорреляционная функция
взаимокорреляционная функция ![]() будет иметь вид или трапеции (при
будет иметь вид или трапеции (при ![]() ), или видтреугольника (
), или видтреугольника (![]() ) (см. рис.17). Теперь перейдем к анализу процессов в описанном фильтре при приеме периодической последовательн
) (см. рис.17). Теперь перейдем к анализу процессов в описанном фильтре при приеме периодической последовательн
ости импульсов. Проведем рассмотрение со спектральной точки зрения. Используем известную связь между спектральной плотностью ![]() одиночного импульса и дискретным спектром периодической последовательности таких импульсов, который описывается рядом Фурье. Связь такова:
одиночного импульса и дискретным спектром периодической последовательности таких импульсов, который описывается рядом Фурье. Связь такова:
где ![]() — комплексная амплитуда катой гармоники спектра периодической последовательности, T- период следования импульсов,
— комплексная амплитуда катой гармоники спектра периодической последовательности, T- период следования импульсов, ![]() .
.
Из формулы следует, что амплитуды гармоник периодической последовательности, умноженные на период Т, равны значениям функции модуля спектра одиночного импульса на частотах ![]() .
.
Для обеспечения оптимального приема периодической последовательности используем опорный сигнал также представляющий периодическую последовательность импульсов с тем же периодом. Таким образом, спектр опорного сигнала будет также дискретным; его гармоники будут иметь те же частоты , что и гармоники спектра входного сигнала.
Каков же будет спектр на выходе умножителя?
Каждая гармоника спектра опорного сигнала в результате перемножения дает суммарную и разностную частоту со всеми гармониками спектра сигнала. Если далее включен фильтр НЧ (![]() ) с полосой более узкой, чем дистанция между гармониками спектров (
) с полосой более узкой, чем дистанция между гармониками спектров (![]() ), то будет выделена сумма постоянных составляющих, получающихся в результате перемножения гармоник спектров на совпадающих частотах. Все остальные комбинационные частоты не будут пропущены таким узкополосным фильтром. Следовательно, суммарный сигнал (как сумма постоянных составляющих) в результате перемножения и фильтрации одинаковых гармоник спектров входного и опорного сигналов будет
), то будет выделена сумма постоянных составляющих, получающихся в результате перемножения гармоник спектров на совпадающих частотах. Все остальные комбинационные частоты не будут пропущены таким узкополосным фильтром. Следовательно, суммарный сигнал (как сумма постоянных составляющих) в результате перемножения и фильтрации одинаковых гармоник спектров входного и опорного сигналов будет
Сравнивая (4.37) с (1.14), видим, что данная сумма описывает взаимокорреляционную функцию периодических сигналов, имеющих одинаковые периоды Т.
Заметим, что данная взаимокорреляционная функция будет описывать периодическое повторение (по переменной t ) полученной выше корреляционной функции для одиночных сигналов (4.34).
Какова же будет амплитудно-частотная характеристика такого фильтра?
В результате простого модельного эксперимента убеждаемся, что рассматриваемый фильтр будет иметь гребенчатую амплитудно-частотную (АЧХ) характеристику. Действительно, представим, что для определения АЧХ подаем на вход испытательный гармонический сигнал ![]() с медленно изменяющейся во времени частотой. Так медленно изменяющейся, чтобы успевал устанавливаться переходной процесс в узкополосном усилителе. При этом обеспечим, что ширина полосы пропускания НЧ фильтра будет много меньше, чем частотный интервал между гармониками в спектре опорного периодического импульсного сигнала. Очевидно, что всякий раз, когда разность частоты какой либо гармоники спектра опорного сигнала и изменяющейся частоты испытательного сигнала оказывается в полосе пропускания НЧ фильтра, на его выходе появляется сигнал. Изменение амплитуды этого сигнала во времени приближенно описывает АЧХ этого низкочастотного фильтра. И так будет всякий раз при прохождении изменяющейся частоты испытательного сигнала
с медленно изменяющейся во времени частотой. Так медленно изменяющейся, чтобы успевал устанавливаться переходной процесс в узкополосном усилителе. При этом обеспечим, что ширина полосы пропускания НЧ фильтра будет много меньше, чем частотный интервал между гармониками в спектре опорного периодического импульсного сигнала. Очевидно, что всякий раз, когда разность частоты какой либо гармоники спектра опорного сигнала и изменяющейся частоты испытательного сигнала оказывается в полосе пропускания НЧ фильтра, на его выходе появляется сигнал. Изменение амплитуды этого сигнала во времени приближенно описывает АЧХ этого низкочастотного фильтра. И так будет всякий раз при прохождении изменяющейся частоты испытательного сигнала ![]() по интервалам
по интервалам ![]() , где
, где ![]() - частоты гармоник спектра (
- частоты гармоник спектра (![]() ) опорного сигнала. Таким образом, в целом полученная АЧХ будет иметь вид «гребенки». Максимумы зубцов этой гребенки будут лежать на частотах
) опорного сигнала. Таким образом, в целом полученная АЧХ будет иметь вид «гребенки». Максимумы зубцов этой гребенки будут лежать на частотах ![]() , ширина же и форма каждого зубца определяются АЧХ узкополосного фильтра, интервалы между зубцами равны интервалам, между гармониками
, ширина же и форма каждого зубца определяются АЧХ узкополосного фильтра, интервалы между зубцами равны интервалам, между гармониками ![]() опорного сигнала.
опорного сигнала.
Особенно явно преимущества корреляционного фильтра, использующего импульсный опорный сигнал, проявятся при приеме радиоимпульсов с высокочастотным заполнением. В этом случае в качестве узкополосного элемента целесообразно использовать резонансный усилитель, обеспечивающий и необходимое усиление сигнала. В этом варианте корреляционный фильтр — это известный супергетеродинный приемник, но с импульсным гетеродином и достаточно узкополосным усилителем промежуточной частоты.
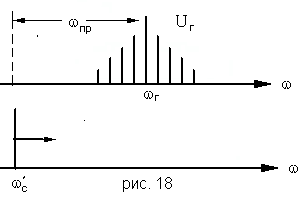
Легко убедиться, что если опорный, (гетеродинный) сигнал это радиоимпульс с несущей частотой ![]() и частотой повторения
и частотой повторения ![]() , то данный приемник-фильтр будет иметь гребенчатую характеристику.
, то данный приемник-фильтр будет иметь гребенчатую характеристику.
Действительно, будем снимать АЧХ устройства, опять подавая на вход смесителя испытательный гармонический сигнал ![]() с медленно изменяющейся частотой. При этом будем использовать импульсный гетеродин и обеспечим, что ширина полосы пропускания резонансного усилителя будет много меньше, чем частотный интервал между гармониками в спектре опорного сигнала — гетеродина
с медленно изменяющейся частотой. При этом будем использовать импульсный гетеродин и обеспечим, что ширина полосы пропускания резонансного усилителя будет много меньше, чем частотный интервал между гармониками в спектре опорного сигнала — гетеродина ![]() . Тогда всякий раз, когда разность (или сумма) текущей частоты испытательного сигнала
. Тогда всякий раз, когда разность (или сумма) текущей частоты испытательного сигнала ![]() с некоторой гармоникой гетеродина оказывается равной
с некоторой гармоникой гетеродина оказывается равной ![]() (в пределах полосы
(в пределах полосы ![]() ) сигнал проходит через узкополосный усилитель. Это будет гармонический сигнал промежуточной частоты с частотой
) сигнал проходит через узкополосный усилитель. Это будет гармонический сигнал промежуточной частоты с частотой ![]() . И так будет повторяться каждый раз, когда разность или сумма частот испытательного сигнала и какой либо изгармоник (n) гетеродина равны
. И так будет повторяться каждый раз, когда разность или сумма частот испытательного сигнала и какой либо изгармоник (n) гетеродина равны ![]()
![]() . Таким образом, очевидно, что амплитудно-частотная характеристика приемника-фильтра будет иметь вид «гребенки». Ширина и форма «зубца» определяется частотной характеристикой узкополосного резонансного усилителя, а положение «зубцов» на шкале частот — положением гармоник гетеродина и номиналом
. Таким образом, очевидно, что амплитудно-частотная характеристика приемника-фильтра будет иметь вид «гребенки». Ширина и форма «зубца» определяется частотной характеристикой узкополосного резонансного усилителя, а положение «зубцов» на шкале частот — положением гармоник гетеродина и номиналом ![]() . Теперь рассмотрим процесс в приемнике-фильтре при включении на его вход периодической последовательности радиоимпульсов. Анализ будем проводить с двух точек зрения: временной и спектральной.
. Теперь рассмотрим процесс в приемнике-фильтре при включении на его вход периодической последовательности радиоимпульсов. Анализ будем проводить с двух точек зрения: временной и спектральной.
Начнем с временной. Предположим, что последовательность импульсов опорного сигнала-гетеродина медленно смещается относительно последовательности входных радиоимпульсов. Такое предположение означает, что частоты повторения импульсов в этих последовательностях отличаются, но так что бы ![]() .
.
На рисунке 19 изображены три относительных положений импульсов во времени.
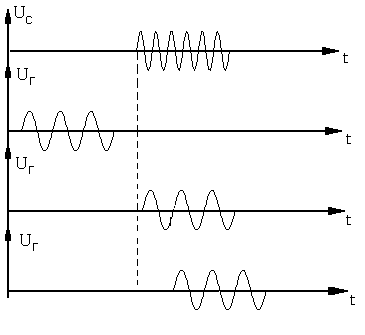
Импульсы частично перекрываются во времени, импульсы совпадают, импульсы разнесены. Очевидно, что во втором случае сигнал промежуточной частоты будет иметь максимальное значение, при разносе их во времени ![]() , а при частичном перекрытии (||) выходной сигнал будет иметь отличное от нуля значение, но
, а при частичном перекрытии (||) выходной сигнал будет иметь отличное от нуля значение, но ![]() . Зависимость амплитуды гармонического сигнала промежуточной частоты от величины их «задержки»
. Зависимость амплитуды гармонического сигнала промежуточной частоты от величины их «задержки» ![]() — относительного положения во времени будет описываться корреляционной функцией, как это было показано выше для одиночных сигналов. Только теперь эта корреляционная функция будет периодической функцией
— относительного положения во времени будет описываться корреляционной функцией, как это было показано выше для одиночных сигналов. Только теперь эта корреляционная функция будет периодической функцией ![]() с периодом Т.
с периодом Т.
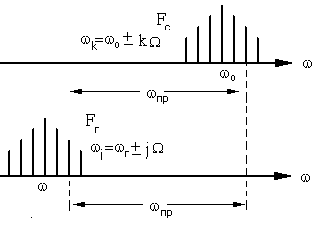
Рассмотрим теперь этот процесс с частотной, спектральной точки зрения. Так как оба сигнала, и входящий, и опорный являются радиоимпульсами с различной несущей (![]() ), но с одинаковыми частотами повторения
), но с одинаковыми частотами повторения ![]() , то каждому соответствует линейчатый (дискретный) спектр с некоторой эффективной шириной. Их спектры разнесены по шкале частот на номинал промежуточной частоты.
, то каждому соответствует линейчатый (дискретный) спектр с некоторой эффективной шириной. Их спектры разнесены по шкале частот на номинал промежуточной частоты.
Для определенности будем считать, что ![]() . Очевидно, что в результате перемножения входного
. Очевидно, что в результате перемножения входного ![]() и опорного
и опорного ![]() каждая из гармоник
каждая из гармоник ![]() даст сумму гармонических сигналов на частотах
даст сумму гармонических сигналов на частотах ![]() . Так как полоса резонансного фильтра принята меньше, чем интервал между гармониками (
. Так как полоса резонансного фильтра принята меньше, чем интервал между гармониками (![]() ), то из богатого спектра комбинационных частот после умножителя узкополосным фильтром будут отфильтрованы только гармонические сигналы с частотами равными промежуточной, т.е.
), то из богатого спектра комбинационных частот после умножителя узкополосным фильтром будут отфильтрованы только гармонические сигналы с частотами равными промежуточной, т.е.
Результирующий гармонический сигнал промежуточной частоты на выходе резонансного фильтра есть векторная сумма „парциальных“ сигналов, получаемых от взаимодействия каждой гармоники спектра ![]() с соответствующей гармоникой спектра опорного гетеродина
с соответствующей гармоникой спектра опорного гетеродина ![]() .
.
Фазы этих „парциальных“ векторов будут различны и изменяться при изменении относительного положения импульсов сигнала и гетеродина во времени. Здесь нужно различать способы формирования опорного (гетеродинного) радиоимпульса.
Первый способ — ударное возбуждение радиоимпульса: фаза ВЧ заполнения жестко привязана к огибающей. При изменении задержки ![]() такой импульс смещается как целое. Фазы гармоник его спектра изменяются так
такой импульс смещается как целое. Фазы гармоник его спектра изменяются так ![]() , т. е. все вектора, представляющие парциальные сигналы, вращаются, но разной „скоростью“.
, т. е. все вектора, представляющие парциальные сигналы, вращаются, но разной „скоростью“.
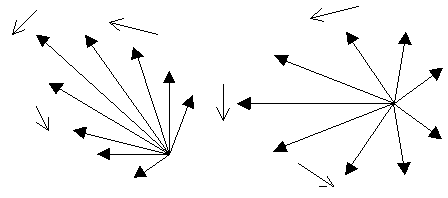
Векторная сумма зависит от взаимного положения „парциальных“ векторов, от их взаимных разностей фаз Качественно картина меняется так: при разносе импульсов во времени эти вектора расположены „веером“ так, что их векторная сумма равна нулю. При частичном перекрытии „веер“ частично „схлопывается“, что дает некоторую отличную от нуля амплитуду суммарного сигнала. Наконец, при совпадении импульсов во времени „веер“ складывается, все „парциальные“ вектора оказываются в фазе, что обеспечивает максимальное значение результирующей амплитуды сигнала промежуточной частоты.
Заметим, что фаза результирующего сигнала промежуточной частоты (положение суммарного вектора) будет изменяться на всем интервале изменения задержки ![]() , от начала „перекрытия“ импульсов (
, от начала „перекрытия“ импульсов (![]() ) во времени, до полного их разноса (
) во времени, до полного их разноса (![]() ).
).
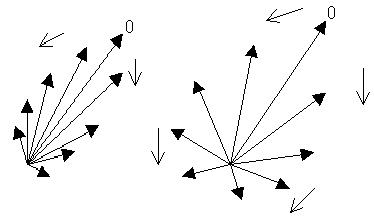
Сказанное качественно иллюстрируется рис. 21,22.
Рассмотрим другой способ формирования опорных радиоимпульсов, импульсов гетеродина. При этом способе из непрерывного гармонического сигнала на частоте ![]() путем импульсной амплитудной модуляции формируется также периодическая последовательность опорных радиоимпульсов. Очевидно, что в этом варианте фаза и огибающая опорных импульсов не будут жестко связаны. Покажем, что при этом фаза сигнала промежуточной частицы на выходе узкополосного резонансного фильтра не будет зависеть от взаимного временного положения периодических последовательностей входного и опорного сигналов. Дело в том, что при формировании опорных импульсов путем модуляции при изменении задержки модулирующего видеоимпульса фаза гармоники на центральной частоте спектра
путем импульсной амплитудной модуляции формируется также периодическая последовательность опорных радиоимпульсов. Очевидно, что в этом варианте фаза и огибающая опорных импульсов не будут жестко связаны. Покажем, что при этом фаза сигнала промежуточной частицы на выходе узкополосного резонансного фильтра не будет зависеть от взаимного временного положения периодических последовательностей входного и опорного сигналов. Дело в том, что при формировании опорных импульсов путем модуляции при изменении задержки модулирующего видеоимпульса фаза гармоники на центральной частоте спектра ![]() остается постоянной. Гармоники же в верхней
остается постоянной. Гармоники же в верхней ![]() и нижней полосах
и нижней полосах ![]() этого спектра будут получать при изменении
этого спектра будут получать при изменении ![]() приращения фаз разных знаков
приращения фаз разных знаков ![]() . Это приводит к тому, что после перемножения со входным сигналом и фильтрации узкополосным резонансным фильтром „парциальных“ сигналов на частоте
. Это приводит к тому, что после перемножения со входным сигналом и фильтрации узкополосным резонансным фильтром „парциальных“ сигналов на частоте ![]() результирующий сигнал на этой частоте не будет изменять своей фазы при изменении задержки. Это утверждение справедливо при условии, что спектры как принимаемого
результирующий сигнал на этой частоте не будет изменять своей фазы при изменении задержки. Это утверждение справедливо при условии, что спектры как принимаемого ![]() , так и опорного (гетеродинного) сигналов симметричны относительно своих несущих частиц ВЧ заполнения. Качественно зависимость параметров выходного сигнала от задержки
, так и опорного (гетеродинного) сигналов симметричны относительно своих несущих частиц ВЧ заполнения. Качественно зависимость параметров выходного сигнала от задержки ![]() так же удобно проиллюстрировать с помощью векторных диаграмм, аналогичных рассмотренным выше.
так же удобно проиллюстрировать с помощью векторных диаграмм, аналогичных рассмотренным выше.
Различие будет лишь в том, что направление (аргумент) вектора парциального сигнала от взаимодействия центральных частот спектров входного и опорного сигналов остается постоянным при изменении задержки на интервале ![]() . Тогда как „парциальные“ вектора , соответствующие верхней и нижней полосам спектров при изменении
. Тогда как „парциальные“ вектора , соответствующие верхней и нижней полосам спектров при изменении ![]() теперь вращаются в разные стороны, образуя опять „веера“. Понятно, что векторная сумма будет зависеть от степени раскрытия такого»веера «, причем аргумент суммарного вектора будет сохранять свою величину, так как „парциальные“ вектора , соответствующие верхней и нижней полосе спектра, получают симметричные приращения, но разных знаков, „Веер“ остается симметричным с неподвижным центральным вектором. Модуль суммарного вектора будет описываться взаимокорреляционной функцией
теперь вращаются в разные стороны, образуя опять „веера“. Понятно, что векторная сумма будет зависеть от степени раскрытия такого»веера «, причем аргумент суммарного вектора будет сохранять свою величину, так как „парциальные“ вектора , соответствующие верхней и нижней полосе спектра, получают симметричные приращения, но разных знаков, „Веер“ остается симметричным с неподвижным центральным вектором. Модуль суммарного вектора будет описываться взаимокорреляционной функцией ![]() и
и ![]() , зависящей от
, зависящей от ![]() .
.
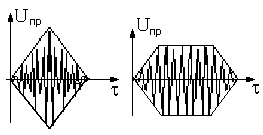
Рассмотрим теперь возможный вариант, когда значения частот заполнения радиоимпульсов принимаемого и опорного совпадают. В этом случае после перемножителя следует включить узкополосный низкочастотный фильтр, выделяющий „постоянную“ составляющую, величина и знак которой будут изменяться при изменении относительного положения принимаемого и опорного импульсов во времени. Такой выходной сигнал будет описываться взаимокорреляционной функцией. Вид этой функции (при равной длительности импульсов) качественно изображен на рис 23. ,а описывается она формулой (4.34). Выходной сигнал в этом случае описывается осциллирующей функцией по аргументу t — относительному сдвигу этих импульсов во времени. Понятно, что для периодически повторяющихся импульсов их взаимокорреляционная функция будет также периодической по t с периодом их следования.

Оценим теперь отношение сигнал/шум на выходе корреляционного гребенчатого
фильтра, оптимального для приёма периодической последовательности радиоимпульсов. Выше было показано, что оптимальный фильтр для гармонического сигнала обеспечивает отношение сигнал/ шум по мощности (4.28)
Гдеb=Dw — полоса узкополосного резонансного фильтра.
В данном случае оптимальный фильтр для приёма периодической последовательности радиоимпульсов имеет также единственный резонансный фильтр с узкой полосой. Поэтому для каждого „зубца“ гребёнки и каждой гармоники спектра входного сигнала будем иметь такое же отношение сигнал/шум, как и для элементарного гармонического сигнала. По отношению к входному сигналу умножитель — это линейное параметрическое устройство. Поэтому результат воздействия спектра гармоник и результат воздействия шума можно рассматривать независимо.
Относительно гармоник спектра сигнала выше было показано, что при совмещении во времени радиоимпульсов входной и опорной последовательностей радиоимпульсов все гармоники парциальных составляющих спектра на частоте ![]() . суммируются в фазе. („веер“ парциальных векторов схлопывается). Составляющие шума, прошедшие отдельные зубцы гребёнки тоже сложатся, но по мощности! Поэтому можно считать, что эффективная полоса для шума будет определяться суммой полос отдельных полос зубцов гребёнки:
. суммируются в фазе. („веер“ парциальных векторов схлопывается). Составляющие шума, прошедшие отдельные зубцы гребёнки тоже сложатся, но по мощности! Поэтому можно считать, что эффективная полоса для шума будет определяться суммой полос отдельных полос зубцов гребёнки: ![]() (4.30).
(4.30).
Число членов в этой сумме ограничено и определяется эффективной шириной спектра опорных радиоимпульсов (импульсов гетеродина). Кроме того, ширина спектра мощности шума ограничивается входным полосовым фильтром. Поэтому искомое отношение сигнал/шум на выходе оптимального корреляционного фильтра определится так:
В заключение обратим внимание, что в рассмотренном варианте гребёнчатая АЧХ реализуется за счёт линейчатого спектра (с некоторой эффективной шириной) импульсного опорного сигнала и единственного узкополосного резонансного усилителя промежуточной частоты. При этом, ширина полосы этого усилителя должна быть много меньше, чем интервал между частотами гармоник опорного сигнала (гетеродина).
Такой аналоговый коррелятор был реализован и практически использовался в станции наклонного зондирования ионосферы средневолнового диапазона. Для возможности оценки не только амплитуды и групповой задержки, но и фазы высокочастотного заполнения отраженных от ионосферы радиоимпульсов после узкополосного усилителя сигнал промежуточной частоты подавался на два параллельных фазовых детектора. Опорные гармонические сигналы на фазовых детекторах имели номинал ![]() и были сдвинуты по фазе на
и были сдвинуты по фазе на ![]() . Таким образом, на выходах фазовых детекторов получались синусная и косинусная составляющие огибающих суммарного сигнала. Это позволяло оценить соответствующие фазовые сдвиги высокочастотного заполнения „земного“ и отраженного радиоимпульсов, при условии, что эти радиоимпульсы были разделены во времени.
. Таким образом, на выходах фазовых детекторов получались синусная и косинусная составляющие огибающих суммарного сигнала. Это позволяло оценить соответствующие фазовые сдвиги высокочастотного заполнения „земного“ и отраженного радиоимпульсов, при условии, что эти радиоимпульсы были разделены во времени.
Пример наблюдаемой картинки на экране индикатора станции приведен на рис. Далее этот сигнал оцифровывался с помощью АЦП и поступал в ЭВМ для обработки.
При используемых параметрах зондирующих радиоимпульсов в диапазоне средних волн „земной“ и отраженный от ионосферы сигналы уверенно разделялись во времени. Величина задержки отраженного сигнала в приводимом эксперименте порядка 220 мкс.
Частота ВЧ заполнения радиоимпульсов приблизительно 350 кГц, приём велся на удалении 220 км. Приёмная аппаратура аналогово коррелятора имела узкополосный усилитель с шириной полосы 5 Гц, при частоте повторения излучаемых импульсов 625 Гц. Это позволяло надёжно выделить полезные сигналы на фоне шумов и помех в весьма загруженном СВ диапазоне, обеспечивался выигрыш в отношении сигнал/шум более30-тина выходе приёмного аналогово коррелятора по отношению ко входу. Очевидно, что располагая сигналом в цифровой форме было возможно и дальнейшее повышение отношения сигнал/шум, используя накопление.
4.5.3. Оценка возможного выигрыша в отношении сигнал / шум при дискретной записи сигнала.
Выше было показано, что для периодического сигнала отношение сигнал / шум может быть улучшено накоплением. Возможный выигрыш пропорционален квадратному корню из времени накопления и обратно пропорционален полосе аналогово фильтра. В случае дискретных отсчётов сигнала — аддитивной смеси сигнал + шум, очевидно, что выигрыш будет пропорционален ![]() , где n число равноотстоящих отсчётов. Процесс накопления удобно реализовать с помощью алгоритма — программы на ЭВМ. При практической реализации этого способа следует иметь в виду, что число накапливаемых выборок, дающих желаемый выигрыш будет ограничено разрядностью применяемого аналого-цифрового преобразователя (АЦП). Можно задаться вопросом о необходимой разрядности АЦП, если задан требуемый выигрыш С / Ш. Или оценить возможный выигрыш, если АЦП уже выбран. Тот факт , что АЦП присущи собственные шумы в данном пособии рассматриваться не будет. Эти вопросы освещены в специальной литературе. Будут учтены только» шумы дискретизации «.
, где n число равноотстоящих отсчётов. Процесс накопления удобно реализовать с помощью алгоритма — программы на ЭВМ. При практической реализации этого способа следует иметь в виду, что число накапливаемых выборок, дающих желаемый выигрыш будет ограничено разрядностью применяемого аналого-цифрового преобразователя (АЦП). Можно задаться вопросом о необходимой разрядности АЦП, если задан требуемый выигрыш С / Ш. Или оценить возможный выигрыш, если АЦП уже выбран. Тот факт , что АЦП присущи собственные шумы в данном пособии рассматриваться не будет. Эти вопросы освещены в специальной литературе. Будут учтены только» шумы дискретизации «.
В этом приближении рассмотрим связь возможного выигрыша С/ Ш при накоплении на АЦП с заданной разрядностью.
Пусть мгновенное значение входной величины есть :
Где U -величина сигнала, ![]() - среднеквадратичная величина шума.
- среднеквадратичная величина шума.
Интересуемся случаем, когда a соответствует максимальному значению числа., минимальный код 1 (число > 0). Считаем, что шумы распределены по нормальному закону.. Ограничим диапазон АЦП утроенной среднеквадратичной величиной шума (3![]() ), что будет соответствовать максимальному коду. Уровень 3
), что будет соответствовать максимальному коду. Уровень 3![]() при нормальном законе распределения ограничит значения шума только в 0.1% случаев. Считая, что динамический диапазон преобразователя установлен 3s, можно ввести коэффициент передачи код -напряжение :
при нормальном законе распределения ограничит значения шума только в 0.1% случаев. Считая, что динамический диапазон преобразователя установлен 3s, можно ввести коэффициент передачи код -напряжение :
Дискретная форма представления числа приводит к»шумам оцифровки «.
Это шум оцифровки, оцениваемый единицей кода , пересчитанной ко входу.
Отношение сигнал / цифровые шумы есть
 или
или Цифровые шумы не снимаются накоплением, поэтому величина b определяет предельно достижимое отношение С / Ш на выходе при данной разрядности , а отношение b/a возможный выигрыш при цифровом
накоплении Оценим теперь возможный выигрыш при данной разрядности. Исходим из того, что при накоплении отношение С / Ш улучшается пропорционально ![]() . Приравнивая эти величины , имеем :
. Приравнивая эти величины , имеем :
Наконец , задаваясь желаемым выигрышем при цифровом накоплении , определяем требуемую разрядность АЦП и ЭВМ .
Полученные приближенные формулы могут оказаться полезными при выборе типа АЦП или при оценке достижимого выигрыша при цифровом накоплении с данным АЦП.
Можно уточнить приведённую оценку» шума оцифровки«- d, если учесть, что как только значение входного сигнала V = U+x окажется вблизи середины шага оцифровки то ,из-за случайного характера шума в АЦП , может быть добавлена или вычтена единица кода. Для приближенной оценки можно на интервале шага оцифровки распределение шума считать равномерным. Тогда дисперсия оцифровки оцениваеtтся так :
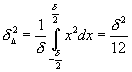
Таким образом реальная величина «шума оцифровки» оказывается меньше.