При обнаружении сигнала на фоне шума наибольшее распространение получил критерий максимума отношения сигнал / помеха на выходе фильтра. Для этого требуется синтезировать фильтр, обеспечивающий в заданный момент времени получение наибольшего возможного отношения пикового значения сигнала к среднеквадратичному значению шума.Сохранение формы сигнала не требуется, так как для обнаружения в шумах форма сигнала значения не имеет.
Будем считать, что сигнал детерминированный , известны его временная функция f(t) и, следовательно, спектр F(
). Шум будем считать стационарным процессом с равномерным энергетическим спетром, то есть шум будем считать «белым» со спектральной плотностью мощности 
.
Задача создания такого оптимального фильтра решается в два этапа :
А) Определение его комплексного коэффициента передачи 
Б) Определение структуры (схемы) фильтра и его параметров.
Коэффициент 
может быть найден для любого физически реализуемого сигнала. Второй этап более сложен и может не иметь решения. Необходимо оценить условия физической осуществимости искомого оптимального фильтра.
Перейдём к конкретному решению первого этапа — определению оптимального
коэффициента передачи фильтра в указанном выше смысле для заданного сигнала и при «белом» шуме. Представив сигнал в виде интеграла Фурье
(п.3.1),( где 
фазовая характеристика спектра сигнала)., а комплексный коэффициент передачи фильтра в виде
Запишем сигнал на выходе фильтра:
(п.3.2)Пусть пик сигнала на выходе фильтра получается в момент 
(пока не известный).
(п.3.3)Теперь оценим мощность шума на выходе этого фильтра.
(п.3.4).Эффективное, среднеквадратичное напряжение шума равно 
.
Следовательно, отношение пикового значения сигнала к напряжению шума
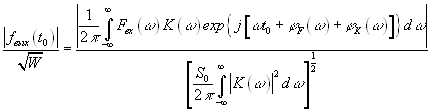(п.3.5).Далее задача заключается в нахождении коэффициента передачи фильтра,
обеспечивающего максимум правой части выражения (3.5). Воспользуемся неравенством Шварца. Для числителя выражения (3.5) можно записать:
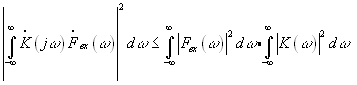(п.3.6)Используя (3.6) , неравенство (3.5) можно записать так :
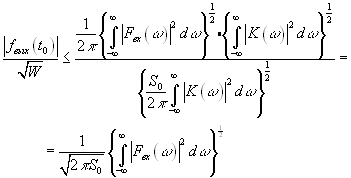(п.3.7)Отсюда видно, что отношение сигнал/шум достигает максимума, когда неравенство (3.7) обращается в равенство. Поскольку правая часть не зависит от 
, для этого необходимо выполнение двух условий (см. (3.3)):
1) чтобы 
. Откуда
(п.3.8).2) чтобы 
, где А постоянный коэффициент. (п.3.9).
Отсюда следует , что коэффициент передачи оптимального фильтра должен иметь вид :
,заметим, что 
есть спектральная функция,
сопряженная спектральной функции сигнала. Поэтому оптимальный коэффициент передачи фильтра будет определяться следующим образом:
. (п.3.10).Заметим, что если 
безразмерная функция, то коэффициент А должен иметь размерность обратную размерности спектра. Из формулы (3.10) следует, что 
. Оптимальный фильтр должен пропускать спектральные составляющие шума неравномерно, с тем большим ослаблением, чем меньше модуль спектра сигнала. В результате полная мощность шума будет меньшей, чем при равномерной амплитудной характеристике. Слагаемое фазовой характеристики 
в (3.8) компенсирует фазовые сдвиги в спектре сигнала. Слагаемое 
обеспечивает появление пика выходного сигнала в момент , то есть задержку выходного сигнала относительно его начала на входе. Только при условии 
может быть использована вся энергия сигнала ,имеющего длительность Т , для создания наибольшего возможного пика в момент
.
Ясно, что дальнейшее увеличение запаздывания не влияет на величину пика.