В разделе 4.2 был рассмотрен вариант алгоритма выделения гармонического сигнала известной частоты из шума, использующий вычисление взаимокорреляционной функции.
. Очевидно, что практически реально осуществить интегрирование при вычислении 
лишь по конечному интервалу времени. Реально это приводит к появлению погрешности,
которая играет роль шума. В формуле (4.8) раздела 4.2 , описывающей функциюсоответствующий *шумовой* член (третий):
(п.4.1)Напомним, что опорный сигнал 
шум. Для оценки величины этого шума используем соотношение Хинчина [12] :
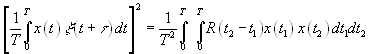(п.4.2).Здесь 
корреляционная функция случайного процесса 
, 
детерминированная функция, в данном случае опорный сигнал. Шум будем считать *белым* со спектральной плотностью мощности 
.Кроме того, будем считать, что на входе коррелятора включен низкочастотный фильтр с коэффициентом передачи
(п.4.3),ограничивающий мощность шума.При таком фильтре и *белом* шуме корреляционная функция случайного процесса была найдена ранее (см. (4.3) раздела (4.2)):
(п.4.4).Подставим функции данного примера под двойной интеграл формулы (п.4.2),
Запишем искомую мощность шума в виде:
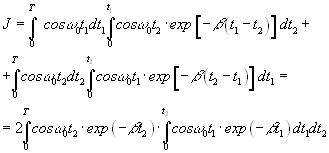(п.4.5).Вычислив этот двойной интеграл, получим величину:
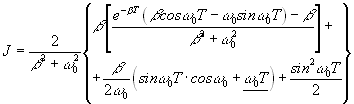(п.4.6).Учтя выражение (п.4.2) в качестве приближенного значения величины J (п.4.6)
ограничимся только членом наиболее медленно убывающем при росте T.
В этом приближении мощность шума на выходе коррелятора будет такой:
(п.4.7),и соответственно среднеквадратичное значение напряжения шума (его*амплитуда*) :
(п.4.8).Напряжение же полезного сигнала , в данном примере это постоянная составляющая, будет иметь величину (см. раздел 4.2 формула (4.8))
(п.4.9).Здесь учтено ослабление сигнала НЧ фильтром. Выбором фазы опорного сигнала 
можно обеспечить 
.Тогда искомое отношение сигнал /шум на выходе коррелятора будет равно:
(п.4.10).Таким образом, *амплитуда* шума (средне квадратичная величина напряжения шума , появляющаяся из-законечного времени интегрирования) на выходе коррелятора будет убывать как 
. Соответственно, отношение сигнал/шум будет расти пропорционально 
.
Заметим, кстати, что величина 
играет роль полосы 
, ограничивающей спектр мощности шума.