Законы сохранения
| Взаимодействие | |||||||
| Электрический заряд, Q | |||||||
| Энергия, E | |||||||
| импульс, p | |||||||
| Угловой момент, J | |||||||
| Барионный заряд, B | |||||||
| Лептонные заряды, | |||||||
| Странность, s | |||||||
| Очарование, c | |||||||
| Красота, b | |||||||
| Истина, t | |||||||
| Изоспин, I | |||||||
| Проекция изоспина, I3 | |||||||
| Пространственная четность, P | |||||||
| Зарядовая четность, C | |||||||
| Временная четность, T | |||||||
| Комбинированная четность, CP | |||||||
| CPT-четность | |||||||
| G-четность | |||||||
В процессе взаимодействий и превращений частиц выполняются определенные законы сохранения. Информация о том, какие величины сохраняются в различных взаимодействиях, приведена выше. Знак «+» («-») показывает, что данная величина сохраняется (не сохраняется). В аддитивных законах сохраняется сумма величин, в мультипликативных законах - произведение величин, которые могут быть равны +1 или -1.
Операция симметрии
Оператор ![]() называют оператором симметрии, если
называют оператором симметрии, если ![]() удовлетворяет тому же самому уравнению Шредингера, что и функция
удовлетворяет тому же самому уравнению Шредингера, что и функция ![]() , а норма
, а норма ![]() равна норме
равна норме ![]() . При этом оператор симметрии
. При этом оператор симметрии ![]() унитарен и коммутирует с гамильтонианом системы
унитарен и коммутирует с гамильтонианом системы 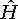 , то есть
, то есть![]() .
.
Сохраняющейся физической величине соответствует эрмитов оператор ![]() , коммутирующий с гамильтонианом.
, коммутирующий с гамильтонианом.
Унитарный оператор ![]() может быть эрмитовым, тогда
может быть эрмитовым, тогда ![]() =
=![]() и
и ![]() . Соответствующая сохраняющаяся величина f может принимать только два значения:
. Соответствующая сохраняющаяся величина f может принимать только два значения: ![]() . Такая симметрия дискретна, а соответствующая сохраняющаяся величина мультипликативна.
. Такая симметрия дискретна, а соответствующая сохраняющаяся величина мультипликативна.
В случае непрерывных симметрий оператор ![]() представим в виде
представим в виде ![]() , где a — вещественный параметр, а
, где a — вещественный параметр, а ![]() — эрмитов. Такими являются операции трансляции, поворотов, калибровочных преобразований…Соответствующие сохраняющиеся величины - импульс, момент количества движения, заряды…
— эрмитов. Такими являются операции трансляции, поворотов, калибровочных преобразований…Соответствующие сохраняющиеся величины - импульс, момент количества движения, заряды…







