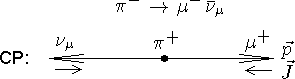4. Зарядовое сопряжение. Зарядовая (С) четность. СР-инверсия

Операция пространственной инверсии в реальном пространстве можно сопоставить операцию инверсии в изоспиновом пространстве. Это приводит к появлению нового мультипликативного квантового числа — «изоспиновой четности» G, эквивалентной четности P реального пространства. Действие оператора G-преобразования можно свести к двум последовательным операциям — зарядовому сопряжению C и повороту на p вокруг оси 2 (или 1) в изоспиновом пространстве, то есть

,

где оператор проекции изоспина на ось 2 изоспинового пространства. G — четность сохраняется только в сильных взаимодействиях.

Зарядовое сопряжение меняет знаки зарядов, оставляя неизменными пространственные переменные, импульс и момент импульса:

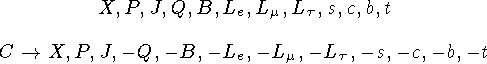
Оператор заряда не коммутирует с оператором зарядового сопряжения . Для заряженных частиц не существует уравнения на собственные з начения оператора зарядового сопряжения:

Это соотношение имеет место только для истинно нейтральных частиц или для систем «частица-античастица». В этом случае

и называется зарядовой четностью.

Зарядовая четность системы «частица-античастица» определяется соотношением

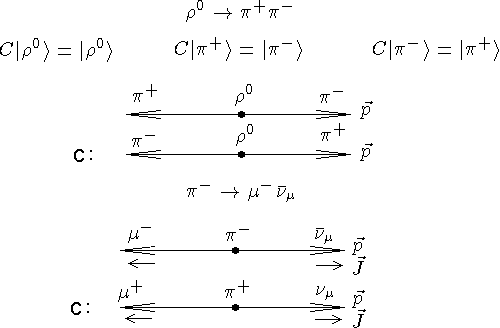
ИзC-инвариантностиследует равенство сечений процессов. В результатеC-инвариантностимы получили ненаблюдаемый в природе процесс. В слабом взаимодействииC-инвариантностьнарушается.

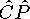
Комбинированная инверсия является последовательной комбинацией преобразований и .
Собственные значения оператора :

Электромагнитные и сильные взаимодействия инвариантны относительно операции комбинированной четности .

Слабые взаимодействия не инвариантны относительно и  преобразований, однако инвариантны относительно операции комбинированной инверсии.