III закон Ньютона

III закон Ньютона

По III закону Ньютона сила F, действующая на тело, является проявлением взаимодействия с некоторым источником, причем само тело действует на источник с силой F’, равной F и направленной в противоположную сторону: F= — F’. Для центрально-симметричных взаимодействий силы действия и противодействия всегда направлены по одной прямой. В общем случае эти силы направлены как показано на рис. A1 

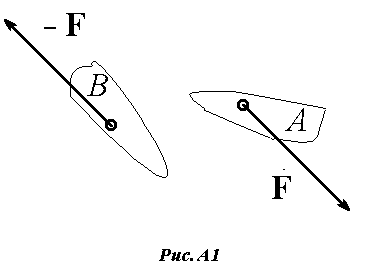
не по линии, соединяющей точки приложения этих сил, а по параллельным линиям. При этом оказывается, что суммарный момент сил в системе двух взаимодействующих тел A и B отличен от нуля!

Докажем, что отличный от нуля момент сил, действующих на некоторую систему из N тел, приводит к изменению ее момента количества движения.
Выпишем уравнения движения для каждого из N тел в следующем виде:

Введенные здесь обозначения очевидны:
F_i — суммарная сила, действующая на тело i; 
v_i и p_i — скорость и импульс этого тела в данный момент;
Dt — промежуток времени, малый настолько, чтобы можно было пренебречь изменением любых параметров системы.
Умножим равенство (A1) слева векторно на радиус-вектор точки приложения силы F_i:

Правую часть этого равенства можно переписать в виде

так как имеет место тождество

Последнее слагаемое в правой части этого тождества обращается в ноль в виду того, что D r_i||p_i (векторное произведение параллельных векторов равно нулю).
Проведем в (A2) суммирование по i:

В левой части этого равенства стоит импульс суммарного момента сил M, а в правой - изменение суммарного момента количества движения L всей системы:

Из этого равенства следует, что отличный от нуля момент сил приводит к изменению вектора момента количества движения системы.
В системе двух тел, изображенной на рис. A1, суммарный момент сил отличен от нуля. Такая система должна, в соответствии с формулой (A3), ускоренно вращаться относительно общего центра масс, что противоречит, в частности, закону сохранения энергии. Могут ли существовать системы, подобные изображенной на рис. A1? 

Сила, действующая на частицу в потенциальном поле, равна

где введен векторный оператор градиента

.

Для центрального-симметричного потенциального поля потенциал взаимодействия двух частиц зависит (по определению) только от расстояния между ними: U(r₁, r₂)=U(|r_1- r₂|). Следовательно, силы взаимодействия частиц F₁ и F₂ равны:

Здесь

.

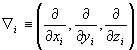Обозначим |r_1- r₂|=r и заметим, что

Таким образом, для центрально-симметричных потенциалов силы действия и противодействия всегда направлены по одной линии в противоположенные стороны. В природе центрально-симметричные потенциалы описывают все дальнодействующие поля - гравитационное и электростатическое. Нецентральные поля (ядерные) имеют конечный радиус взаимодействия (^-13см) и не проявляются в макроскопической физике.

Тем не менее центрально-симметричные потенциалы могут приводить к нецентральным взаимодействиям. Приведем конкретный пример такой системы. Заряд q расположим на расстоянии L от середины диполя, состоящего из зарядов +q и -q, как показано на рис. A2. Дл ина диполя dL.

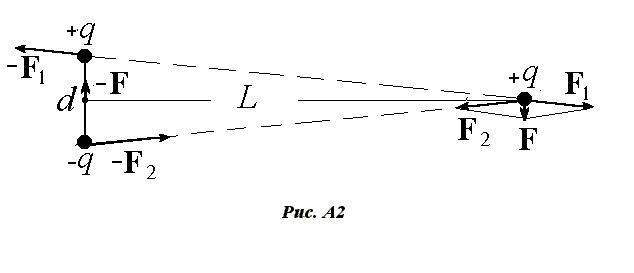
Силы F₁ и F₂, действующие на заряд со стороны диполя, равны по величине. Их векторная сумма равна F. Силы, действующие на диполь со стороны заряда, равны -F₁ и -F₂ соответственно, а их сумма -F. Момент сил F и -F относительно любой точки отличен от нуля, направле н по часовой стрелке и равен M=FL. Но заметим, что момент сил -F₁ и -F₂, п риложенных к диполю, тоже отличен от нуля, направлен против часовой стрелки и равен M’@ F₁d. Из сравнения треугольника сил F₁, F₂, F с треугольником, в вершинах которого находятся заряды, видим, что F ₁/F@ L/d. Отсюда получаем, что F₁d @ FL и M=M’, а в векторной форме M=- M’. Следовательно, суммарный момент сил, действующих в этой системе, равен нулю.
Заряд, находящийся в точке B, действуя на диполь, расположенный в точке A, создает не только силу - F, но и момент сил - M’.

Покажем, что потенциальное поле, создаваемое диполем, нецентральное.

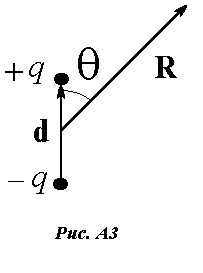
Для этого обратимся к рис. А3 и вычислим потенциал в произвольной точке на расстоянии R от центра диполя под углом q к вектору d, соединяющему заряды диполя:

Это выражение на расстояниях R>>d можно упростить, используя разложение по малой величине d/R:

С учетом этого приближения формула (A8) может быть переписана в виде

Для элементарного диполя d- 0, q стремится к бесконечности при фиксированном значении дипольного момента p=qd. Потенциал поля такого диполя

Видим, что потенциальное поле диполя не обладает сферической симметрией — потенциал явно зависит не только от расстояния R до диполя, но и от угла q между осью диполя и направлением в точку наблюдения.
Таким образом, даже в центрально-симметричных потенциальных полях взаимодействие элементарных объектов может иметь вид, характерный для нецентральных потенциалов. Силы действия и противодей ствия равны, направлены противоположно, но не по одной прямой, соединяющей точки приложения сил, а по параллельным линиям. При этом взаимодействие в целом описывается не только силами, но и моментами сил, т. е. имеет более сложный вид, чем обычно подразумевается при формулировке III закона.