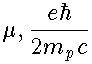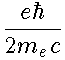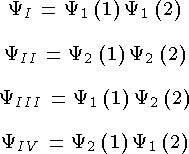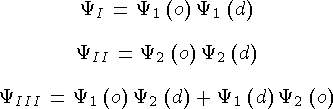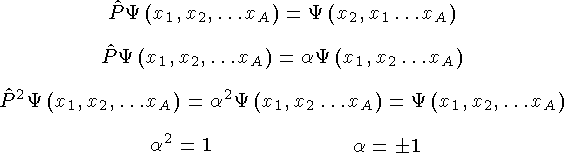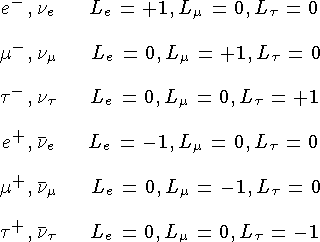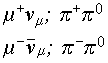(материалы к лекциям по ядерной физике для студентов 3 курса физического факультетатеоретические группы)
Представленные здесь материалы являются дополнением к лекциям по ядерной физике и физике элементарных частиц, читающихся студентам третьего курса в весеннем семестре на физических факультетах МГУ и СПбГУ. Это не курс лекций, а лишь краткое его содержание с основными формулами, графиками и фотографиями. Цель этого материала v дать студентам возможность после занятий просмотреть содержимое лекций, в том числе и материал, не поддающийся конспектированию (графики, схемы и т.д.).
- Систематика частиц. Фермионы, бозоны. Лептоны, адроны, калибровочные бозоны.
- Законы сохранения в мире частиц.
- Пространственная инверсия. Р-четность.
- Зарядовое сопряжение. Зарядовая (С) четность. СР-инверсия.
- Обращение времени. СРТ-теорема.
- Частицы и античастицы.
- Резонансные частицы.
- Изоспин частиц и ядер. Изоспиновые мультиплеты.
- Странность. Рождение и распад странных частиц.
- Слабые взаимодействия. Промежуточные бозоны.
- Несохранение четности в слабых взаимодействиях.
- Слабые распады лептонов
- Нейтрино и антинейтрино. Спиральность.
- Кварковая структура адронов. Барионы. Мезоны.
- Кварки. Глюоны. Цвет.
- Слабые распады кварков.
- Возбужденные состояния нуклонов.
- Объединение взаимодействий. Нестабильность протона.
- Дейтрон.
- Свойства нуклон-нуклонного взаимодействия.
- Мезонная теория ядерных сил.
- Электромагнитные взаимодействия. Структура нуклона.
- Опыт Резерфорда. Состав и размер ядра.
- Масса и энергия связи ядра. Энергия отделения нуклонов.
- Формула Вайцзеккера для энергии связи ядра.
- Модель ядерных оболочек.
- Одночастичные и коллективные возбуждения ядра.
- Ядерные реакции (законы сохранения, кинематика).
- Механизмы ядерных реакций. Прямые реакции. Составное ядро.
- Синтез и деление ядер. Ядерная энергия.
- Квадрупольный электрический момент и форма ядра.
- Спиновый и орбитальный ядерный магнетизм. Ядерный магнетон.
- Законы радиоактивного распада ядра.
- Альфа-распад. Кулоновский и центробежный барьеры.
- Бета-распад. Экспериментальное обнаружение нейтрино.
- Гамма-излучение ядер. Электрические и магнитные гамма-переходы.
- Эффект Мессбауэра.
- Нуклеосинтез во Вселенной. Ядерные реакции в звездах.
- Космические лучи. Их состав и происхождение.
В представленных материалах использованы
- Б.С.Ишханов, Физика ядра и частиц, конспект лекций, МГУ, 1997
- W.von Schlippe, Theory of Angular Momentum in Quantum Mechanics, Lecture Notes. SPbSU, 1999
- W.von Schlippe, Collider Physics, Lecture Notes. SPbSU, 1999
- W.von Schlippe, Basics of Relativistic Kinematics, Lecture Notes, SPbSU, 1998
- W.von Schlippe, Relativistic Quantum Mechanics, Lecture Notes, SPbSU, 1999
- Г. Фрауэнфельдер, Э. Хенли. «Субатомная физика» — М., Мир. 1979
- Д. Блан, Ядра, частицы, ядерные реакторы. М., Мир. 1989
- Д. В. Сивухин «Общий курс физики», т. 5, ч. 2: «Атомная и ядерная физика» — М., Наука . 1989
Опыт Райнеса и Коуэна, 1954г.
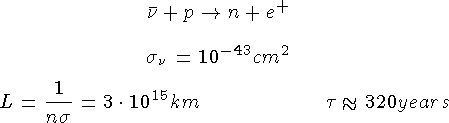
Слабые взаимодействия удобно изучать в реакциях с нейтрино — частицами, участвующими только в слабых взаимодействиях или в распадах, запрещенных в сильных и электромагнитных взаимодействиях. Впервые экспериментально прямая регистрация антинейтрино была осуществлена в опытах Райнеса и Коуэна. Наблюдались задержанные совпадения импульсов от аннигиляции позитрона (e+) и радиационного захвата нейтрона кадмием.
Мюонное нейтрино nm
В эксперименте 1962 г. было показано, что нейтрино и антинейтрино, рождающиеся в распаде m-->мезон ов не тождественны нейтрино и антинейтрино, образующимся в процессе b-распада.
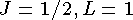
| Частица |
Масса |
Время жизни |
| nm |
< 17 MeV |
стабильно |
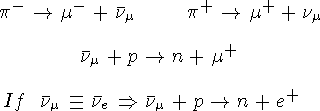
t-лептон, 1975 г.
t-лептонбыл открыт в 1975 г. по наблюдению аномальных событий типа 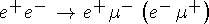 . t -лептон по своим свойствам аналогичен e, m и характеризуется лептонным числом Lt .
. t -лептон по своим свойствам аналогичен e, m и характеризуется лептонным числом Lt .
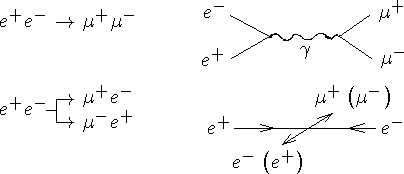
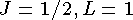
| Частица |
Масса |
Время жизни (сек) |
| t |
1778 МэВ |
2.9·10-13 с |
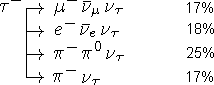
Гипотеза W-бозона
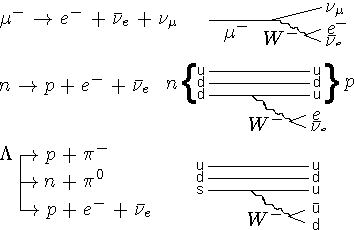
Слабый изоспин
| |
e |
ne |
e+ |
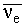 |
| T |
1/2 |
1/2 |
1/2 |
1/2 |
| T3 |
-1/2 |
1/2 |
1/2 |
-1/2 |
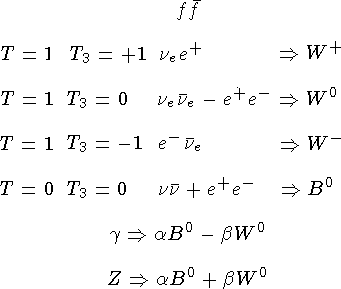
Нейтральные слабые токи.
По аналогии с изоспином, введенным в случае сильных взаимодействий, объединим в единый слабый мультиплет фермионные дублеты 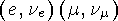 -
- 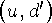 ча стицы, рождаемые W-бозоном. Слабое взаимодействие включает фермион-антифермионные пары. Из инвариантности слабого взаимодействия относительно вращений в слабом изоспиновом пространстве наряду с полями переносчиками
ча стицы, рождаемые W-бозоном. Слабое взаимодействие включает фермион-антифермионные пары. Из инвариантности слабого взаимодействия относительно вращений в слабом изоспиновом пространстве наряду с полями переносчиками 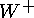 >и
>и 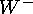 >бозонами необходимо ввести третье поле
>бозонами необходимо ввести третье поле 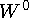 >с нулевым эл ектрическим зарядом. Реакции, идущие в результате обмена
>с нулевым эл ектрическим зарядом. Реакции, идущие в результате обмена 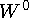 >бозоном, называют слабыми процессами с сохранением заряда или нейтральными слабыми токами. Из состояний
>бозоном, называют слабыми процессами с сохранением заряда или нейтральными слабыми токами. Из состояний 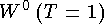 >и
>и 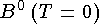 >можно построить 2 суперпозиции
>можно построить 2 суперпозиции
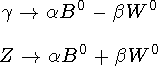 ,
,
соответствующие фотону и 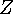 -бозону.
-бозону. 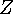 >-бозон был открыт в 1983 г.
>-бозон был открыт в 1983 г.
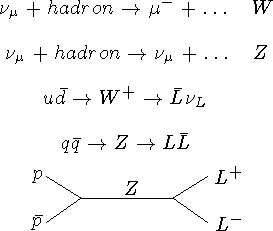
Странные частицы
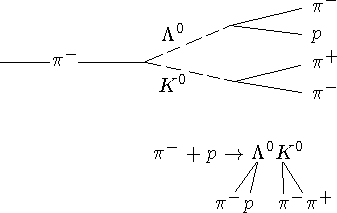
| Частица |
Масса, mc2, МэВ |
Спин-четность, изоспин, JP(I) |
Время жизни t или ширина G |
| L |
1116 |
1/2+(0) |
2.6×10-10 |
| S+ |
1189 |
1/2+(1) |
0.8×10-10 |
| S0 |
1193 |
1/2+(1) |
7.4×10-20 |
| S- |
1197 |
1/2+(1) |
1.5×10-10 |
| X0 |
1315 |
1/2+(1/2) |
2.9×10-10 |
| X- |
1321 |
1/2+(1/2) |
1.6×10-10 |
| W- |
1672 |
1/2+(0) |
0.8×10-10 |
| K0 |
498 |
0-(1/2) |
KL: 5.2×10-8KS: 0.9×10-10 |
Странность, s
Квантовое число s может принимать значения -3, -2, -1, 0, 1, 2, 3 и определяется кварковым составом адронов. Частицы, в сос тав которых входит странный кварк, называются странными частицами. Сохранение странности в сильных и электромагнитных взаимодействиях проявляется в особенности их рождения и распада. Странные частицы в сильных и электромагнитных взаимодействиях как прави ло рождаются парами. Характерное время жизни странных частиц10—10 с. Это объясняется тем, что в слабых распадах странность может не сохраняться. Барионы L, S, X, W со странностью, отличной от нуля, называются гиперонами.
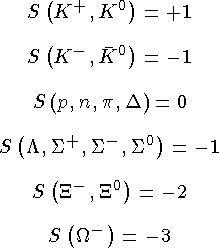
В сильных и электромагнитных взаимодействиях странность сохраняется
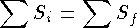
В слабых взаимодействиях странность не изменяется или изменяется на единицу
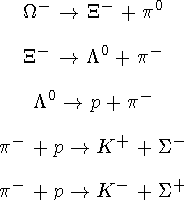
Шарм, c
Квантовое число c может принимать значения -3, -2, -1, 0, 1, 2, 3 и определяется кварковым составом адронов. Адроны с о тличным от нуля числом c называются очарованными частицами.
| Частица |
Масса, mc2 (МэВ) |
Время жизни t (сек) или ширина G (МэВ) |
Спин-четность, изоспин, JP(I) |
| J/Y |
3097 МэВ |
0.088 МэВ |
1-(0) |
В сильных взаимодействиях квантовое число c сохраняется. В слабых взаимодействиях оно либо сохраняется, либо изменяется на единицу: Dc= 0, ¦1.
Bottomness, b
Красота (beauty, bottomness) b. Квантовое число b может принимать значения -3, -2, -1, 0, 1, 2, 3 и зависит от числа b кварков и антикварков в составе адрона.
| Частица |
Масса, mc2 (МэВ) |
Время жизни t (сек) или ширина G(МэВ) |
Спин-четность, изоспин, JP(I) |
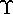 |
9460 |
0.0525 МэВ |
1-(0) |
В сильных взаимодействиях квантовое число b сохраняется. В слабых взаимодействиях оно либо сохраняется, либо изменяется на единицу
Как наблюдать резонансы?
- Максимумы в сечении.
- Восстановление инвариантной массы.
Время жизни резонанса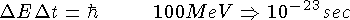
Нуклонные резонансы
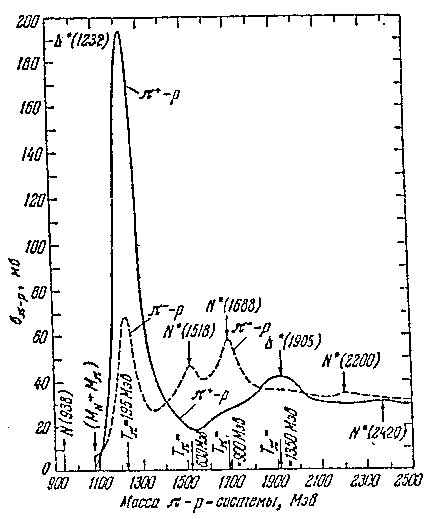
В сечении сильновзаимодействующих частиц наблюдаются резонансы — коротко живущие возбужденные состояния адронов, распадающиеся в результате сильного взаимодействия. Характерное время жизни резонанса10—2 2 —10—24 сек. Впервые резонансы наблюдались в сечении взаимодействия p-, p+ — мезонов с нуклонами. Масса резонансной частицы M определяется из релятивистского инварианта
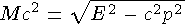 ,
,
где E и p- полная энергия и полный импульс p-мезона и нуклона. Ма ксимумы в сечении p-N рассеяния интерпретируются как появление нестабильной частицы - резонанса - с вполне определенными квантовыми характеристиками: массой, зарядом, спином, изоспином и др. Резонансы наблюдаются и во взаимодействии p-мезонов.
| |
JP(I) |
Масса, МэВ |
G, МэВ |
распады |
| D(1232) |
3/2+(3/2) |
1232 |
120 |
Np |
| N(1520) |
3/2-(1/2) |
1520 |
120 |
Np, Npp, Dp |
p-p, p+p рассеяние
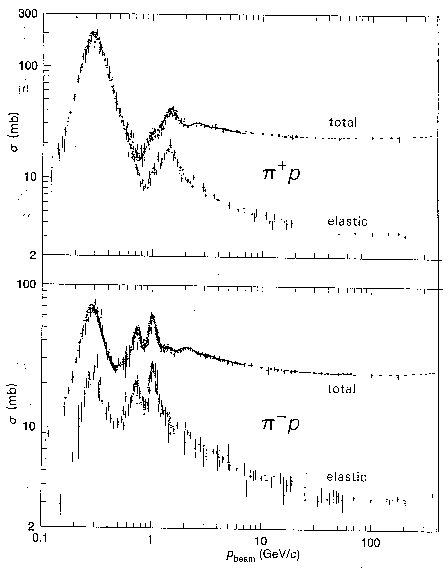
| Система |
p-p |
p+p |
| I3 |
-1+1/2 |
1+1/2 |
| I |
1/2, 3/2 |
3/2 |
Античастицы
Каждая частица имеет своего двойника — античастицу. Античастицы обладают рядом характеристик, имеющих те же значения, что и частица — масса, спин, время жизни, и некоторые характе ристики с противоположным знаком — электрический заряд, барионное и лептонные числа, s, c, b, t.
Связь характеристик частиц и античастиц
| Характеристика |
Частица |
Античастица |
| Масса |
M |
M |
| Электрический заряд |
+(-)Q |
-(+)Q |
| Спин |
S |
S |
| Магнитный момент |
+(-)m |
-(+)m |
| Барионное число |
+B |
-B |
| Лептонное число |
+Le, +Lm, +Lt |
-Le, -Lm, -Lt |
| Странность |
+(-)s |
- (+)s |
| Charm |
+(-)c |
- (+)c |
| Bottomness |
+(-)b |
- (+)b |
| Topness |
+(-)t |
- (+)t |
| Изоспин |
I |
I |
| Проекция изоспина |
+(-) I3 |
- (+)I3 |
| Четность |
+(-) |
- (+) |
| Время жизни |
T |
T |
| Схема распада |
 |
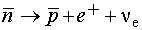 |
АНТИПРОТОН, 1955 г.
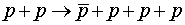
АНТИНЕЙТРОН, 1956 г.
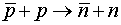
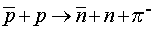
K-мезоны
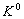 и
и 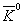 - мезоны обладают удивительными свойствами. Они резко отличаются по своим свойствам в сильных взаимодействиях и почти не различ имы в слабых. Эта специфика обусловлена тем, что единственное квантовое число, которым они различаются, — странность:
- мезоны обладают удивительными свойствами. Они резко отличаются по своим свойствам в сильных взаимодействиях и почти не различ имы в слабых. Эта специфика обусловлена тем, что единственное квантовое число, которым они различаются, — странность:
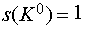 ,
, 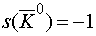 .
.
Это позволяет системе 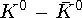 совершать уникальные превращения, которые служат иллюстрацией основного принципа квантовой механики — линейная суперпозиция двух состояний также являе тся состоянием системы. Состояния
совершать уникальные превращения, которые служат иллюстрацией основного принципа квантовой механики — линейная суперпозиция двух состояний также являе тся состоянием системы. Состояния

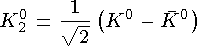
имеют определенные значенияCP-четности.
Наблюдение в 1964 г. распада 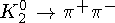 :
:
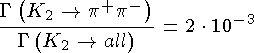
означает нарушение CP-четностив слабых распадах 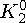 -мезонов. Была введена еще одна комбинация K0 и
-мезонов. Была введена еще одна комбинация K0 и 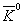 мезонов:
мезонов:
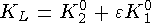
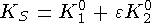 .
.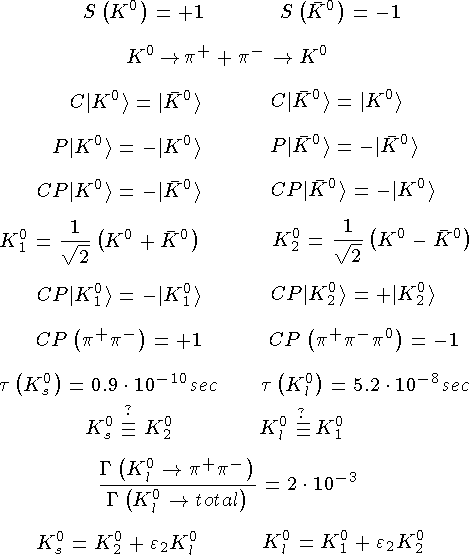
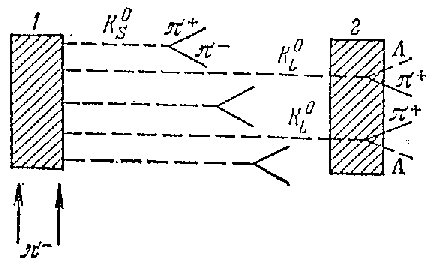
Опыт Пайса-Пиччиони
В опыте Пайса-Пиччиони наблюдались осцилляции 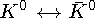 в пучке K0-мезонов.
в пучке K0-мезонов.
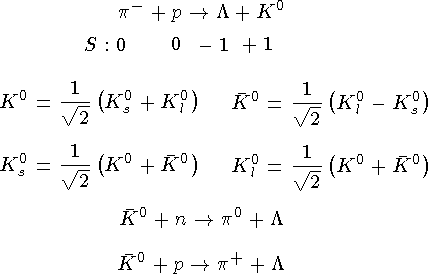
Обращение времени, T

Свободное движение (J=0)
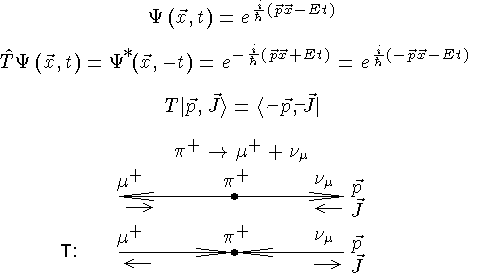
CPT-преобразование
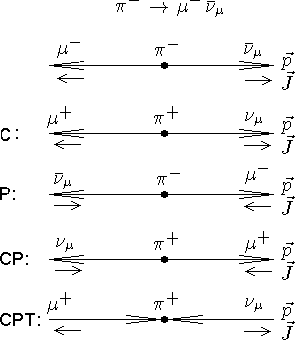
G — четность
Операция пространственной инверсии в реальном пространстве можно сопоставить операцию инверсии в изоспиновом пространстве. Это приводит к появлению нового мультипликативного квантового числа — «изоспиновой четности» G, эквивалентной четности P реального пространства. Действие оператора G-преобразования можно свести к двум последовательным операциям — зарядовому сопряжению C и повороту на p вокруг оси 2 (или 1) в изоспиновом пространстве, то есть
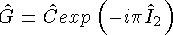 ,
,
где 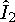 оператор проекции изоспина на ось 2 изоспинового пространства. G — четность сохраняется только в сильных взаимодействиях.
оператор проекции изоспина на ось 2 изоспинового пространства. G — четность сохраняется только в сильных взаимодействиях.
Зарядовое сопряжение, 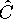
Зарядовое сопряжение 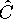 меняет знаки зарядов, оставляя неизменными пространственные переменные, импульс и момент импульса:
меняет знаки зарядов, оставляя неизменными пространственные переменные, импульс и момент импульса:
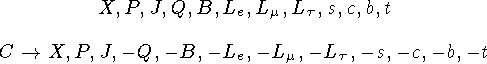
Оператор заряда 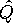 не коммутирует с оператором зарядового сопряжения
не коммутирует с оператором зарядового сопряжения 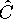 . Для заряженных частиц не существует уравнения на собственные з начения оператора зарядового сопряжения:
. Для заряженных частиц не существует уравнения на собственные з начения оператора зарядового сопряжения:
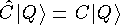
Это соотношение имеет место только для истинно нейтральных частиц или для систем «частица-античастица». В этом случае

и называется зарядовой четностью.
Зарядовая четность системы «частица-античастица» определяется соотношением
C=(- 1)L+S= (- 1)I+1
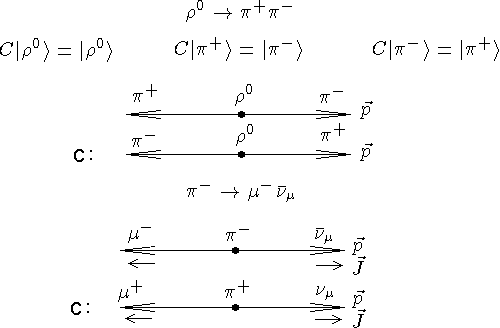
ИзC-инвариантностиследует равенство сечений процессов. В результатеC-инвариантностимы получили ненаблюдаемый в природе процесс. В слабом взаимодействииC-инвариантностьнарушается.
Комбинированная инверсия, 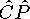
Комбинированная инверсия является последовательной комбинацией преобразований 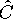 и
и 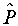 .
.
Собственные значения оператора 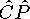 :
:
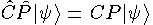
Электромагнитные и сильные взаимодействия инвариантны относительно операции комбинированной четности 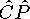 .
.
Слабые взаимодействия не инвариантны относительно 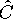 и
и 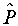 преобразований, однако инвариантны относительно операции комбинированной инверсии.
преобразований, однако инвариантны относительно операции комбинированной инверсии.
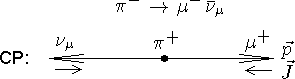
Пространственная четность Р характеризует свойства системы относительно пространственных отражений. Различают состояния с положительной и отрицательной четностью. Четность волновой функции Р частицы определяется моментом l и внутренней четностью Рi и равна Р = Рi (-1)l. Четность — мультипликативное квантовое число. Протоны и нейтроны имеют положительную внутреннюю четность, поэтому четность ядра определяется соотношением 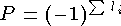 , где li — орбитальные моменты нуклонов в ядре.
, где li — орбитальные моменты нуклонов в ядре.
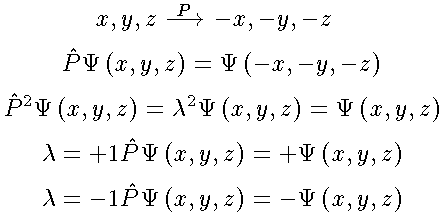
Четность в сферической системе координат:
PYlm=(-1)lYlm
Четность системы частиц:
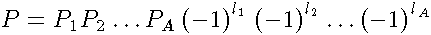
Пространственная четность, P
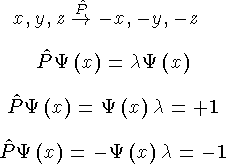
Закон сохранения четности: если оператор четности коммутирует с оператором гамильтона, то имеет место закон сохранения четности — четность системы сохраняется. В случае сильных и электромагнитных взаимодействий:
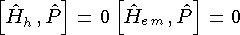
В слабом взаимодействии четность не сохраняется. В результате слабого взаимодействия система может переходить из состояния с одной четностью в состояние противоположной четности:
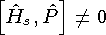
P-преобразование
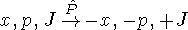
Распад r0-мезона (сильное взаимодействие)

Распад p+-мезона (слабое взаимодействие)
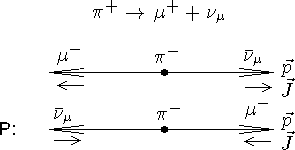
Из P-инвариантности следует равенство сечений процессов. В результате P-преобразования возникла ситуация, ненаблюдаемая в природе - антинейтрино с отрицательной спиральностью. Следовательно, в слабых взаимодействиях P-инвариантность нарушается.
Законы сохранения
| Взаимодействие |
Сильное |
Электромагнитное |
Слабое |
| Аддитивные законы сохранения: |
| Электрический заряд, Q |
+ |
+ |
+ |
| Энергия, E |
+ |
+ |
+ |
| импульс, p |
+ |
+ |
+ |
| Угловой момент, J |
+ |
+ |
+ |
| Барионный заряд, B |
+ |
+ |
+ |
| Лептонные заряды, |
+ |
+ |
+ |
| Странность, s |
+ |
+ |
- |
| Очарование, c |
+ |
+ |
- |
| Красота, b |
+ |
+ |
- |
| Истина, t |
+ |
+ |
- |
| Изоспин, I |
+ |
- |
- |
| Проекция изоспина, I3 |
+ |
+ |
- |
| Мультипликативные законы сохранения: |
| Пространственная четность, P |
+ |
+ |
- |
| Зарядовая четность, C |
+ |
+ |
- |
| Временная четность, T |
+ |
+ |
- |
| Комбинированная четность, CP |
+ |
+ |
- |
| CPT-четность |
+ |
+ |
+ |
| G-четность |
+ |
- |
- |
В процессе взаимодействий и превращений частиц выполняются определенные законы сохранения. Информация о том, какие величины сохраняются в различных взаимодействиях, приведена выше. Знак «+» («-») показывает, что данная величина сохраняется (не сохраняется). В аддитивных законах сохраняется сумма величин, в мультипликативных законах - произведение величин, которые могут быть равны +1 или -1.
Операция симметрии
Оператор 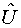 называют оператором симметрии, если
называют оператором симметрии, если 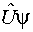 удовлетворяет тому же самому уравнению Шредингера, что и функция
удовлетворяет тому же самому уравнению Шредингера, что и функция 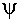 , а норма
, а норма 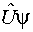 равна норме
равна норме 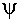 . При этом оператор симметрии
. При этом оператор симметрии 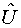 унитарен и коммутирует с гамильтонианом системы
унитарен и коммутирует с гамильтонианом системы 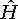 , то есть
, то есть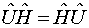 .
.
Сохраняющейся физической величине соответствует эрмитов оператор 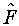 , коммутирующий с гамильтонианом.
, коммутирующий с гамильтонианом.
Унитарный оператор 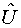 может быть эрмитовым, тогда
может быть эрмитовым, тогда 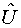 =
=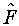 и
и 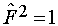 . Соответствующая сохраняющаяся величина f может принимать только два значения:
. Соответствующая сохраняющаяся величина f может принимать только два значения: 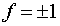 . Такая симметрия дискретна, а соответствующая сохраняющаяся величина мультипликативна.
. Такая симметрия дискретна, а соответствующая сохраняющаяся величина мультипликативна.
В случае непрерывных симметрий оператор 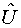 представим в виде
представим в виде 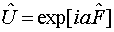 , где a — вещественный параметр, а
, где a — вещественный параметр, а 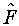 — эрмитов. Такими являются операции трансляции, поворотов, калибровочных преобразований…Соответствующие сохраняющиеся величины - импульс, момент количества движения, заряды…
— эрмитов. Такими являются операции трансляции, поворотов, калибровочных преобразований…Соответствующие сохраняющиеся величины - импульс, момент количества движения, заряды…
Относительная сила взаимодействий
| Взаимо-действие |
Характернаяконстантавзаимо-действия |
Частицы, участвующиево взаимо-действии |
Квантывзаимо-действия |
Массакванта(ГэВ) |
Характерноевремявзаимо-действия (с) |
Характерныйрадиусвзаимо-действия (см) |
| Сильное |
1 |
Кварки(адроны) |
Глюон |
0 |
10—23-10—25 |
¦ 10—13 |
| Электромагнитное |
10—2 |
Заряженные частицы |
gквант |
0 |
10—18 |
infinite |
| Слабое |
10—6 |
Все частицы |
W¦ -бозон,Z0-бозон |
80—91 |
10—12 |
10—16 |
| Гравита-ционное |
10—38 |
Все частицы |
Гравитон-? |
0 |
|
infinite |
Характеристики нейтрона, протона и электрона.
| |
n |
p |
e |
| Масса, МэВ/c2 |
939.6 |
938.3 |
0.511 |
Спин,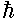 |
1/2 |
1/2 |
1/2 |
| Заряд,(4.8·10—10 CGSE) |
0 |
+1 |
-1 |
Магнитный момент, 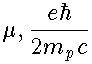 |
-1.91 |
2.79 |
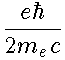 |
| Период полураспада |
10.4 мин. |
Стаб. |
Стаб. |
Схема распада нейтрона: 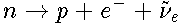
Статистика
Статистика — свойство системы тождественных частиц. Статистика является следствием принципа неразличимости частиц одного сорта (тождественных частиц) и вероятностного характера событий в микромире.
2 частицы (1, 2). 2 состояния (y1, y2).
Классический случай
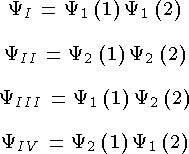
Статистика Бозе-Эйнштейна
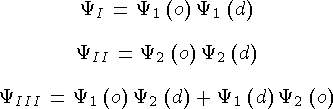
Статистика Ферми-Дирака
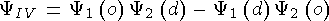
Принцип Паули

Многочастичный случай
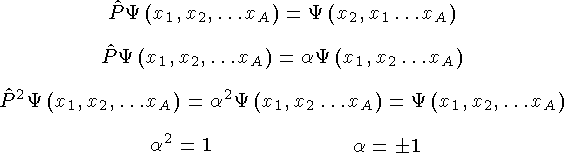
Симметричные состояния a = +1.
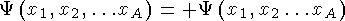
Статистика Бозе-Эйнштейна. Бозоны (J = 0, 1, 2, …).
Антисимметричные состояния a = -1.
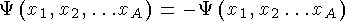
Статистика Ферми-Дирака. Фермионы (J = 1/2, 3/2, …).
Барионный заряд, B
Все сильновзаимодействующие частицы (адроны) с полуцелым спином имеют барионный заряд B=+1. Адроны с целым спином (мезоны) — B =0. Сильновзаимодействующие античастицы с полуцелым спином имеют B=-1. В замкнутой системе барионный заряд сохраняется.
Адроны
Частицы, участвующие в сильных взаимодействиях, называются адронами. Они подразделяются на барионы, имеющие барионный заряд B=1, и мезоны, для которых B=0. Барионы являются фермионами (имеют полуцелый спин), мезоны являются бозонами (имеют нулевой или целочисленный спин). Адроны также характеризуются квантовыми числами s (странность), c (очарование), b (красота), t (истина), изоспином I и его третьей проекцией I3. Лептоны не участвуют в сильных взаимодействиях, имеют спин 1/2 и лепто нные заряды Le, Lm, Lt.
Законы сохранения
| Взаимодействие |
Сильное |
Электромагнитное |
Слабое |
| Аддитивные законы сохранения: |
| Электрический заряд, Q |
+ |
+ |
+ |
| Энергия, E |
+ |
+ |
+ |
| импульс, p |
+ |
+ |
+ |
| Угловой момент, J |
+ |
+ |
+ |
| Барионный заряд, B |
+ |
+ |
+ |
| Лептонные заряды, |
+ |
+ |
+ |
| Странность, s |
+ |
+ |
- |
| Очарование, c |
+ |
+ |
- |
| Красота, b |
+ |
+ |
- |
| Истина, t |
+ |
+ |
- |
| Изоспин, I |
+ |
- |
- |
| Проекция изоспина, I3 |
+ |
+ |
- |
| Мультипликативные законы сохранения: |
| Пространственная четность, P |
+ |
+ |
- |
| Зарядовая четность, C |
+ |
+ |
- |
| Временная четность, T |
+ |
+ |
- |
| Комбинированная четность, CP |
+ |
+ |
- |
| CPT-четность |
+ |
+ |
+ |
| G-четность |
+ |
- |
- |
В процессе взаимодействий и превращений частиц выполняются определенные законы сохранения. Информация о том, какие величины сохраняются в различных взаимодействиях, приведена выше. Знак «+» («-») показывает, что данная величина сохраняется (не сохраняется). В аддитивных законах сохраняется сумма величин, в мультипликативных законах — произведение величин, которые могут быть равны +1 или -1.
Таблица частиц
Лептоны 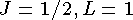
| Частица |
Масса |
Время жизни |
| ne |
< 7 eV |
стабильно |
| nm |
< 0.17 MeV |
стабильно |
| nt |
< 24 MeV |
стабильно |
| e |
0.511 MeV |
>4.3×1023 лет |
| m |
105.66 MeV |
2.2x10—6 с |
| t |
1777 MeV |
2.9x10—13 с |
L — лептонное число
Лептонные числа Le, Lm, Lt
Лептонные числа Le, Lm, Ltприсваивают частицам, образующим группу лептонов. Лептонные числа Le, Lm, Lt имеют значения, равные -1, 0, 1. Лептоны не участвуют в сильных взаимодействиях.
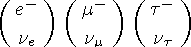
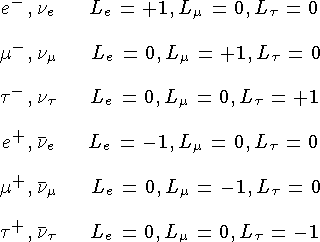
Лептонные числа Le, Lm, Ltс охраняются во всех видах взаимодействий
Промежуточные бозоны 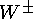 ,
, 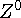 , 1983 г.
, 1983 г.
| Частица |
Масса |
Время жизни, ширина |
Спин J |
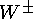 |
80.33 ГэВ |
2.07 ГэВ |
1 |
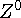 |
91.19 ГэВ |
2.49 ГэВ |
1 |
Мезоны (B=0)
| Частица |
Масса, mc2, МэВ |
Время жизни t или ширина G |
Спин-четность, изоспин, JP(I) |
Основные моды распада |
| p¦ |
139.57 |
2.6×10-8с |
0-(1) |
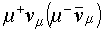 |
| p0 |
134.98 |
8.4×10-17 с |
0-(1) |
2g |
| K¦ |
494 |
1.2×10-8 с |
0-(1/2) |
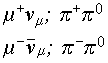 |
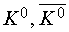 |
498 |
KL 5.2×10-8 сKS 0.9×10-10 с |
0-(1/2) |
KL: p+p-p0; p0p0p0KS : p+p-; p0p 0 |
| h |
547 |
1.18 КэВ |
0-(0) |
2g; 3p0 |
| r¦ , r0 |
770 |
150 МэВ |
1-(1) |
2p |
| w |
782 |
8.4 МэВ |
1-(0) |
3p |
| j |
1019 |
4.4 МэВ |
1-(0) |
2K |
| J/y |
3097 |
87 КэВ |
1-(0) |
адроны; e+e-; m+m- |
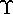 |
9460 |
52 КэВ |
1-(0) |
адроны; e+e-; m+m-; t+t - |
Барионы (B=1)
| Частица |
Масса, mc2, MeV |
Время жизни t или ширина G |
Спин-четность, изоспин, JP(I) |
Основные моды распада |
| p (N+) |
938.27 |
>1.6×1025 лет |
1/2+(1/2) |
|
| n (N0) |
939.57 |
887 c |
1/2+(1/2) |
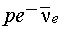 |
| L |
1116 |
2.6×10-10 с |
1/2+(0) |
np0; pp- |
| S+ |
1189 |
0.8×10-10 с |
1/2+(1) |
np+; pp0 |
| S0 |
1193 |
7.4×10-20 с |
1/2+(1) |
Lg |
| S- |
1197 |
1.5×10-10 с |
1/2+(1) |
np- |
| X 0 |
1315 |
2.9×10-10 с |
1/2+(1/2) |
Lp0 |
| X - |
1321 |
1.6×10-10 с |
1/2+(1/2) |
Lp- |
| W- |
1672 |
0.8×10-10 с |
3/2+(0) |
LK-; X 0p-; X -p0 |
| D++, D+, D0, D- |
1230 |
0.9 MeV |
3/2+(3/2) |
Np |










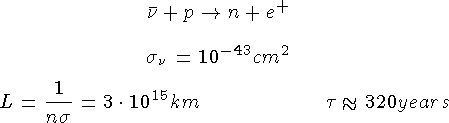
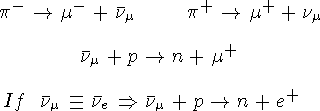
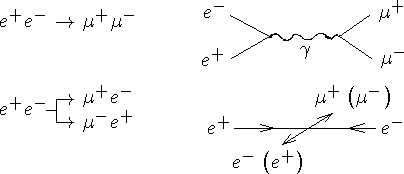
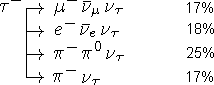
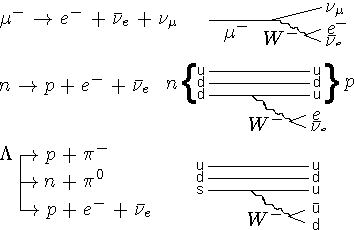
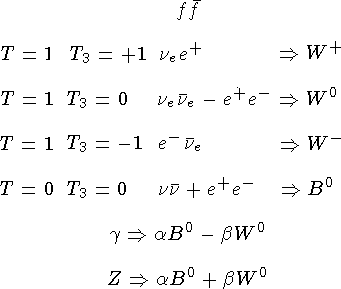
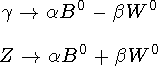 ,
,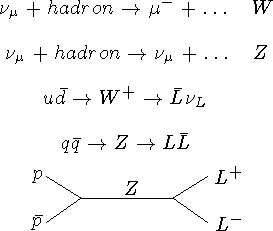

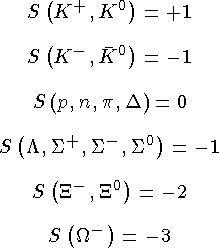
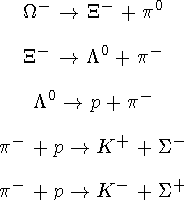


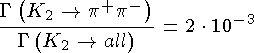
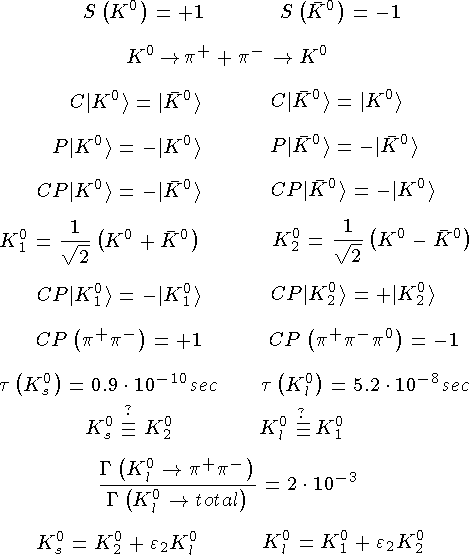

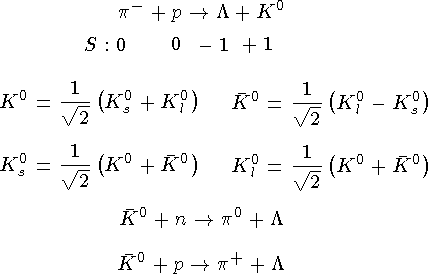

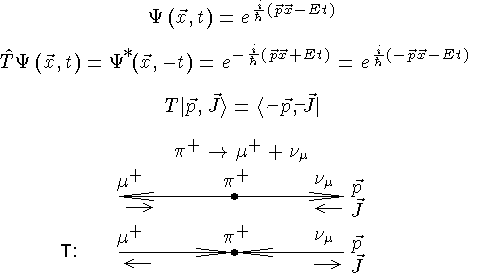
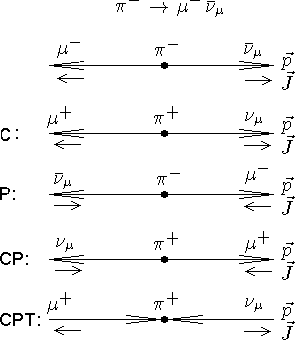
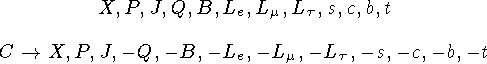
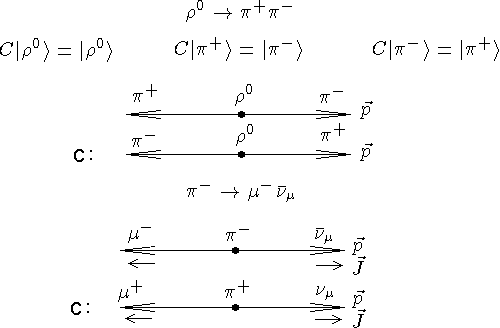
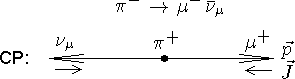
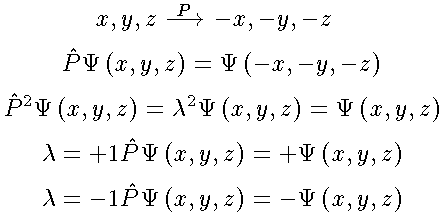
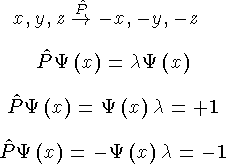

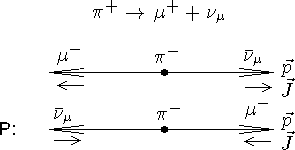
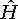 , то есть
, то есть