Функции когерентности B(t) и корреляции R(t), определяющие связь двух значений случайной величины в произвольные моменты времени, были определены через двумерную плотность распределения вероятности [ см. (1.6), (1.7),(1.8) основного текста].
Для эргодических процессов эти же функции были определены усреднением произведения двух текущих значений случайного процесса при сдвинутых аргументах. [см.(1.12) основного текста ].
Приведём доказательство основных свойств корреляционных функций.
1.Из определения этих функций (1.6) , (1.12) следует, что при t=0
 — мощность случайного процесса.
— мощность случайного процесса.
2. Функция корреляции четная функция.
 Действительно :
Действительно :
 .
.
3. Функция R(t) есть невозрастающая функция.

Это свойство следует из равенства: . Или
. Или
 , беря среднее по времени от обеих частей этого равенства, получаем:
, беря среднее по времени от обеих частей этого равенства, получаем: .
.
4. Функция корреляции детерминированного процесса.
Пример 1.


Заметим , что при конечном времени интегрирования Т корреляционная функция имеет член, описывающий осцилляции по аргументу , убывающие как 1/T.
, убывающие как 1/T.
Пример 2. Функция корреляции для детерминированной перидической функции.

Так как функция x (t) представлена рядом по полной системе ортогональных функций, то в результате вычисления интегралов (аналогичных тому, который был вычислен в предыдущем примере) будут не равны нулю лишь члены с одинаковыми частотами. Это даст для искомой корреляционной функции следующий результат:

Аналогично можно убедиться, что и взаимная корреляционная функция двух периодических функций будет содержать только те частоты, которые имеются в обеих функциях.
7. Статистические критерии обнаружения сигналов в шумах
В ряде задач приёма сигналов в присутствии шумов нельзя ограничиться таким общим критерием, как отношение сигнал / шум. Возникает необходимость использовать более тонкие статистические свойства процессов, которые дают возможность количественно оценить достоверность полученных данных. (например, о координатах объекта по сигналам РНС или координатах цели по данным радиолокатора). Вследствие случайного характера помех принципиально невозможно добиться их полного устранения. Использование рассмотренных выше «оптимальных» фильтров меняет характеристики случайного процесса, но процесс остаётся случайным. Путём совершенствования приёмных устройств можно снизить вероятность ошибки только до некоторого уровня . [13 ].
В данном пособии ограничимся изложением классической задачи обнаружения сигнала. Пусть на выходе приёмного устройства имеется некий сигнал — случайный процесс:
U(t) = V(t) + z (t) (7.1)
Этот процесс может представлять либо только шумы — z(t) . либо сумму детерминированного сигнала V(t) и шума. Будем считать, что факт наличия сигнала V(t) тоже случаен.
Для решения вопроса о наличии сигнала в данный момент можно принять правило: сигнал присутствует, если U (t) > E, т.е. превышает некоторый уровень, порог и что сигнал отсутствует в противоположном случае. U(t)
Ошибочный ответ может быть дан в двух несовместимых между собою случаях :1) когда сигнал отсутствует, V(t) = 0, но напряжение шума превышает уровень Е. (событие А = «ложная тревога» .- Л.Т.) 2) Когда сигнал присутствует, V(t) 0, но сумма сигнала и шума не превышает уровня U(t) Б, «пропуск сигнала»).
Вероятность ложной тревоги (событие А), т. е. того, что будут совмещены два события — отсутствие сигнала и превышение шумом уровня Е ( при отсутствии сигнала) , равна априорной вероятности отсутствия сигнала, умноженной на апостериорную вероятность превышения уровня Е, при условии, что сигнал отсутствует. Априорной вероятностью q отсутствия сигнала зададимся, а апостериорную вероятность превышения шумом уровня Е легко получить по одномерной функции распределения шума W(x).
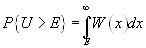
, тогда
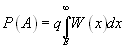
(7.2)
Вероятность того, что будут совмещены два события — присутствие сигнала и непревышение суммарным напряжением уровня Е (вероятность события Б) равна априорной вероятности присутствия сигнала, умноженной на апостериорную вероятность непревышения уровня Е при условии, что сигнал присутствует. Априорная вероятность присутствия сигнала равна:
Апостериорную вероятность непревышения уровня Е можно получить, используя одномерную функцию распределения суммы сигнала и шума — 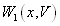 .
.
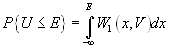
, тогда
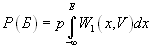
(7.3),
Так как события А и Б несовместимы, то вероятность ошибочного ответа Р(А или Б) равна:
Р(А или Б) = Р(А) + Р(Б) =
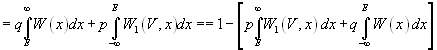 (7.4).
(7.4). Следовательно, искомая вероятность правильного ответа 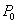 равна:
равна:
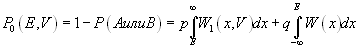
(7.5)
Возникает вопрос: как выбрать пороговый уровень Е? Ясно, что если уровень выбрать высоким , то вероятность Р(А) — ложной тревоги будет мала, но вероятность пропуска имеющегося сигнала будет велика. Наоборот, при низком уровне Е мала будет вероятность пропуска сигнала, но будет значительной вероятность ложной тревоги Р (А).Эти качественные рассуждения можно облечь в количественные соотношения, зависящие от конкретной задачи.
Может быть поставлена задача нахождения оптимальной величины порога Е, для которого вероятность правильного ответа (7.5) при заданных функциях распределения сигнала и шума максимальна. Вычисляя производную выражения (7.5) по Е и приравнивая её нулю, получаем уравнение для определения оптимального уровня:
Статистический критерий (7.6), обеспечивающий максимальную вероятность правильного ответа при одном или нескольких измерениях , называется критерием «идеального наблюдателя».
Как следует из уравнения (7.6), определяемый уровень зависит от вида функций распределения.
Рассмотрим решение этого уравнения на примере обнаружения положительной телеграфной посылки (положительного импульса с амплитудой V) на фоне шума, подчиняющемуся нормальному закону распределения, с дисперсией 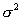 . Наличие или отсутствие сигнала скажется только на среднем значении суммарного сигнала (7.1).
. Наличие или отсутствие сигнала скажется только на среднем значении суммарного сигнала (7.1).
Соответственно плотности распределения будут иметь вид:
Смысл выбора порога (см. уравнение 7.6) иллюстрируется рис.3.7 .
Рис. 36 Рис.37
Оптимальный уровень определяется точкой пересечения графика (1) — 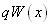 распределения шума с графиком (2) -
распределения шума с графиком (2) -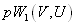 совместного распределения сигнала и шума.( с учётом масштабных коэффициентов q,p). Как видно из рисунка 3.7 , при сильном сигнале уровень Е должен выбираться высоким, а при слабом этот уровень приближается к среднеквадратичному напряжению шума.
совместного распределения сигнала и шума.( с учётом масштабных коэффициентов q,p). Как видно из рисунка 3.7 , при сильном сигнале уровень Е должен выбираться высоким, а при слабом этот уровень приближается к среднеквадратичному напряжению шума.
В случае, когда априорная вероятность появления сигнала неизвестна, часто полагают р=1/2, считая, что априорно равновероятно, как наличие, так и отсутствие сигнала. (заметим, что при этом q=1/2 тоже). Тогда для распределений (7.7) величина порога оказывается равной Е= V/2. ( См. Рис 3.6).
Если уровень Е выбран, то для рассматриваемого примера, где плотность распределения вероятностей шума и сигнала с шумом определены выражениями (7.7), для вероятностей ложной тревоги и пропуска сигнала, используя (7.2) и (7.3), получаются выражения:
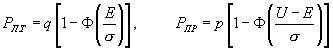
(7.8).
Здесь
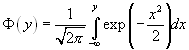
- функция Крампа [6].
На практике обычно интересуются не вероятностью пропуска сигнала, а вероятностью правильного обнаружения D (при условии, что превышен уровень Е):
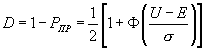
( при p=1/2).

.(7.9).
Приведём другой пример. Подлежащий определению сигнал является огибающей суммарного высокочастотного колебания, которое вызвано как воздействием шума, так и полезного высокочастотного сигнала (радиоимпульса).
При воздействии одного шума плотность распределения огибающей r высокочастотного колебания описывается функцией Релея:
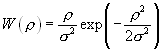
при
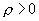
, и
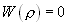
при
r
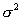 - дисперсия шума.
- дисперсия шума.
При совместном воздействии шума и высокочастотного сигнала огибающая
имеет плотность распределения, подчиняющуюся закону Релея — Райса:
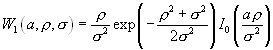
, при
r>0 (7.11).
и 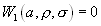 , при r модифицированная функция Бесселя.
, при r модифицированная функция Бесселя.
Рис.38
Графики функций (7.10) и (7.11) приведены на рис. 38.
Если в этом примере опять принять p=q, то оптимальный уровень опять определится точкой пересечения кривой распределения шума с кривой совместного распределения сигнала и шума. Из рисунка видно: при сильном сигнале уровень Е должен выбираться высоким, а при слабом сигнале этот уровень приближается к среднеквадратичному напряжению шума. При p q масштабы графиков функций (7.10) и (7.11) соответственно изменятся, но оптимальный уровень будетпо-прежнемуопределяться уравнением (7.6).то есть точкой пересечения соответствующих графиков.
Рассмотренный критерий идеального наблюдателя, когда как ложное обнаружение, так и пропуск сигнала нежелательны в одинаковой степени, наиболее характерен для систем радиосвязи.
В радиолокационных системах обнаружения используется другой критерий, называемый критерием Неймана-Пирсона. Использование другого критерия объясняется тем, что ложное обнаружение цели может иметь весьма нежелательные последствия. Поэтому вероятность ложной тревоги должна быть весьма малой, обычно задаются её значением порядка 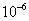 -
-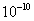 . Часто её значение не может быть увеличено даже учитывая то , что при этом снижается вероятность обнаружения сигнала. Итак, при использовании критерия Неймана-Пирсона вероятность ложной тревоги фиксируется изначально. Так как вероятность ложной тревоги функционально связана с относительным порогом, то последний также оказывается заданным
. Часто её значение не может быть увеличено даже учитывая то , что при этом снижается вероятность обнаружения сигнала. Итак, при использовании критерия Неймана-Пирсона вероятность ложной тревоги фиксируется изначально. Так как вероятность ложной тревоги функционально связана с относительным порогом, то последний также оказывается заданным
Практически стараются удовлетворить одновременно двум противоречивым требованиям : 1) чтобы вероятность Р(Б) пропуска сигнала не превосходила некоторой величины [Р(Б)
Левый график изображает функцию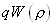 , а правый -
, а правый -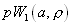 .
.
Рис.39
Вертикальная линия, восстановленная из точки соответствующего значения относительного порога (E/s), совместно с графиками ограничивает площади, соответствующие вероятностям Р(А) и Р(Б).Они отмечены разной штриховкой.. Приведенные графики позволяют качественно проанализировать различные ситуации. Так при увеличении отношения сигнал /шум (а/s) график функции 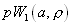 будет смещаться вправо(смотри рис.38). Поэтому для сохранения допустимой величины Р(Б) -вероятности пропуска сигнала, окажется возможным увеличить относительный порог E/s. При этом площадь Р(А) — вероятность ложной тревоги уменьшится! Верно и обратное.
будет смещаться вправо(смотри рис.38). Поэтому для сохранения допустимой величины Р(Б) -вероятности пропуска сигнала, окажется возможным увеличить относительный порог E/s. При этом площадь Р(А) — вероятность ложной тревоги уменьшится! Верно и обратное.
Поэтому единственной возможностью увеличения вероятности правильного обнаружения цели остаётся повышение отношения сигнал /шум на входе порогового устройства , т. е. на выходе линейного тракта приёмного устройства. Эти вопросы были рассмотрены в предыдущих разделах. Методики расчета конкретных радиотехнических устройств и количественных оценок вероятностных характеристик приема реальных флуктуирующих сигналов в присутствии шума достаточно сложны и изложены в специальной литературе.
Рассмотрим возможность использования стохастического характера среды распространения электромагнитных волн для определения параметров сигнала. Конкретно рассмотрим возможность оценки отношения амплитуд «земного» и отраженного от ионосферы сигналов при распространении электромагнитных волн в волноводном канале Земля — ионосфера. Будут рассмотрены два альтернативных метода : метод моментов и метод максимального правдоподобия.
Для использования этих методов существенно выполнение следующих условий:
-
в точке приёма электромагнитное поле представляется суммой двух волн «земной» , распространяющейся вдоль земной поверхности и однократно отраженной от ионосферы,
-
принимается гипотеза о типе (характере) плотности распределения амплитуды отраженного сигнала.
Далее определяются параметры плотности распределения суммарного сигнала. Естественно, что эти условия, даже приближенно, выполняются только в ограниченной области частот, электрических свойств земной поверхности и ионосферы.
Модель односкачкового распространения адекватно описывает условия распространения электромагнитных волн в средневолновом и длинноволновом диапазонах ( на частотах 0.1 — 1.5 мГц) при распространении над сухопутными трассами протяжённостью в сотни километров. При этом амплитуды многократно отраженных волн оказываются относительно малыми и полное поле определяется суммой «земной» и однократно отраженной волн. Такая модель подтверждается экспериментально при анализе принимаемых импульсных щирокополосных сигналов, когда оказывается возможным разделение этих волн вследствие запаздывания отраженной волны. Ранее выполненные эксперименты с импульсными сигналами позволили установить, что ортогональные компоненты отраженного сигнала в большинстве случаев распределены нормально и независимо, причем практически с нулевым средним. Отсюда следует, что амплитуда суммарного сигнала подчиняется закону распределения Рэлея-Райса [ ].
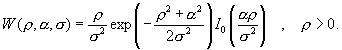
(6.1)
где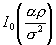 - модифицированная функция Бесселя нулевого порядка.
- модифицированная функция Бесселя нулевого порядка.
Параметрами функции (6.1) являются: амплитуда земного сигнала (a),
( её считаем детерминированной, не подверженной случайным флуктуациям), среднеквадратичная величина амплитуды отраженного сигнала s и величина амплитуды суммарного сигнала r . Равенство s = 0 соответствует отсутствию отраженного сигнала.
Задача состоит в том, чтобы из экспериментально полученной реализации суммарного сигнала определить параметры a иs .
В качестве источников сигнала можно использовать обычные радиовещательные станции, выделяя при приёме только амплитуду суммарного сигнала на несущей частоте.
Отражающая верхняя граница волновода — ионосфера подвержена случайным флуктуациям, поэтому электромагнитное поле отраженной волны — случайный процесс, вообще нестационарный. При выборе временного интервала анализа следует иметь в виду, что должны быть удовлетворены противоречивые требования. Действительно, с одной стороны, интервал анализа должен быть минимальным, чтобы не потерять естественные природные вариации свойств ионосферы и чтобы на этом интервале процесс можно было считать стационарным. Это позволяет использовать классическую теорию стационарных случайных процессов. С другой стороны, интервал между отсчётами при измерениях должен превышать время корреляции случайного процесса, чтобы эти отсчёты были независимыми. Кроме того, понятно, что для получения статистических оценок на интервале «стационарности» необходимо иметь представительное число отсчётов. Возможность удовлетворения указанным противоречивым требованиям зависит от конкретного физического процесса. В результате обработки данных эксперимента с широкополосными импульсными радиосигналами было установлено: время корреляции амплитуд отраженных сигналов составляет единицы минут. Поэтому интервал выборки для анализа должен быть не менее десятков минут. При увеличении его сверх этого интервала может быть не оправдана гипотеза о стационарности процесса. На восходе и заходе Солнца этот интервал должен быть уменьшен до минут.
6.1 Метод моментов.
Считая, что закон распределения плотности вероятности (1) выполняется для экспериментально зарегистрированных амплитуд суммарного сигнала, строятся поверхности первого и второго моментов (Рис. 29 ? 30)по данным выборки над плоскостью параметров a и s .По известным формулам[6]:
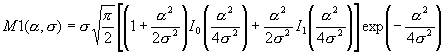
, (6.2)
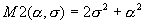
, (6.3)
где I0, I1 — модифицированныефункции Бесселя нулевого и первого порядка.
Далее, сравнивая реальные, полученные по данным эксперимента , М1* и М2* с предвычисленными для наборов значений (a, s), подбирается пара параметров aк, sк таких, чтобы значения предвычисленных и экспериментальных моментов оказались равными ( с точностью до шага вариации аргумента функций (6.2), (6.3) при вычислениях).
Практически подбор искомых параметров aк, sк осуществляется следующим образом. Плоскостями, соответствующими найденным из эксперимента значениям моментов М1* и М2*, проводятся сечения поверхностей моментов М1 и М2, априорно построенных по их вычисленным значениям для набора (сетки) параметров (aк, s к). Эти сечения, проектируясь на плоскость параметров, дают изолинии, как функции этих параметров.
Точка пересечения изолинии первого и второго моментов на этой плоскости и даёт искомые значения параметров, которые обеспечивают равенство априорно вычисленных моментов М1 , М2 со значениями М1*, М2*, найденными из эксперимента.
Рис.29, Рис.30
Математическое моделирование эксперимента показало работоспособность этого метода. Наиболее информативными являются первый начальный и второй центральный моменты. Это связано с тем, что для двух начальных моментов при реально ограниченной выборке изолинии пересекаются под острым углом и результат получается с большим разбросом Рис.31. А при использовании при обработке центрального второго момента , отраженный от ионосферы сигнал уверенно отделялся от «земного» даже при его относительно малой амплитуде.
Рис. 31
Очевидно, что конкретное расположение проекций сечений поверхностей М1, М2 плоскостями М1* и М2* и, следовательно, угол пересечения этих проекций зависит от величин моментов, полученных по данным эксперимента. Таким образом, результаты определения a, s могут иметь различную точность.
Рис.32
Работоспособность метода моментов подтвердилась и при обработке данных реальных экспериментов. В качестве примера на рис 6.4 изображена гистограмма амплитуд суммарного сигнала радиостанции * Маяк* на частоте 549кГц и построенный по найденным параметрам график функции плотности распределения Релея — Райса (1). Полученное совпадение можно считать приемлемым (рис.6.4). Недостатком рассмотренного метода моментов является также и то, что отсутствуют теоремы, позволяющие охарактеризовать свойства получаемых оценок параметров.
6.2. Метод максимального правдоподобия
Для решения рассматриваемой задачи об определении отношения амплитуд *земного* и отраженного сигналов на основе статистических характеристик суммарного сигнала может быть использован и широко известный метод максимального правдоподобия. При использовании этого метода будем также считать, что огибающая суммарного сигнала случайная величина r, распределённая по закону Рэлея-Райса. Плотность распределения вероятности этой случайной величины описывается выражением (6.1):
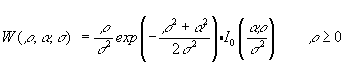
(6.1).
Здесь a — амплитуда земного сигнала (в конкретном эксперименте постоянная величина), s — среднеквадратическая амплитуда отраженного от ионосферы сигнала, r — амплитуда суммарного сигнала, регистрируемая в эксперименте.
Максимально правдоподобной оценкой называется та, которая максимизирует так называемую функцию правдоподобия — плотность вероятности выборки (выборка — это набор из N независимых измерений величин 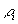 ). Так как измерения независимы, то эта плотность вероятности равна произведению плотностей вероятности отдельных её элементов. Учитывая большой динамический диапазон плотностей распределения, на практике оказывается удобным рассматривать логарифмы соответствующих величин. Тогда вместо произведения плотностей вероятности максимизировать сумму их логарифмов, учитывая монотонность этой функции.
). Так как измерения независимы, то эта плотность вероятности равна произведению плотностей вероятности отдельных её элементов. Учитывая большой динамический диапазон плотностей распределения, на практике оказывается удобным рассматривать логарифмы соответствующих величин. Тогда вместо произведения плотностей вероятности максимизировать сумму их логарифмов, учитывая монотонность этой функции.
Рассмотрим два варианта приложения метода максимального правдоподобия к задаче определения отношения амплитуд *земного* и отраженного сигналов. В первом варианте предполагается возможность измерения отдельно амплитуды *земной* волны. Это может быть возможно при некоторых условиях (частота сигнала, протяженность трассы и др.) в дневное время. При продолжении измерений в ночное время появляется отраженная волна и принимается уже суммарный сигнал . Таким образом, единственным параметром, требующим определения, оказывается отношение амплитуды отраженного сигнала к амплитуде *земного* .(g).В выражении (6.1) перейдём к новым переменным : 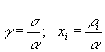 . Тогда можем записать для плотности вероятности в безразмерных величинах:
. Тогда можем записать для плотности вероятности в безразмерных величинах:
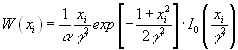
(6.4).
Прологарифмировав функцию (6.4), а затем просуммировав по всем измеренным 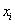 , получим искомый логарифм функции правдоподобия:
, получим искомый логарифм функции правдоподобия:
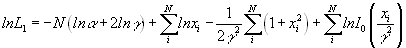
(6.5).
Задача теперь состоит в том, чтобы найти при каком g эта функция максимальна, то есть какое g наиболее вероятно.
Во втором варианте, когда возможно измерение только амплитуды суммарного сигнала, имеем два неизвестных параметра — амплитуды *земного* и отраженного сигналов. В этом случае удобно также перейти к безразмерным величинам: 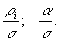 После логарифмирования суммирования функционал примет следующий вид:
После логарифмирования суммирования функционал примет следующий вид:
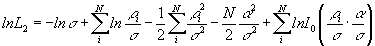
(6.6).
Данный функционал нужно максимизировать по двум параметрам, чтобы найти интересующее отношение амплитуд *земного* и отраженного сигналов.
6.3. Практические результаты
Приведём примеры обработки данных сеанса измерений по методу правдоподобия в обоих вариантах. Анализировались сигналы радиостанции Finnradio (558 кГц), расположенной от пункта наблюдения на расстоянии 260 км. В этих условиях, как показали предварительно выполненные расчёты, а также прямые наблюдения, в дневных условиях отражённый от ионосферы сигнал практически отсутствовал. Амплитуда *земного* сигнала стабильна и равна 990 ед. АЦП. Поэтому можно было применить первую однопараметрическую модификацию метода. На рис 6.5 приведён график логарифма одномерной функции правдоподобия для одного из ночных сеансов с использованием найденной ранее величины (a).
Рис.33
Уверенно выделяется максимум при g = 0.175, что соответствует амплитуде отраженного сигнала s = 173 ед. АЦП.
Использование второго варианта метода иллюстрируется результатом обработки данных этого же сеанса наблюдений
Вычислялся логарифм двумерной функции правдоподобия для того же промежутка времени, но в предположении, что не известны обе амплитуды. На рис.6.6 изображён рельеф функции (6.5)- двухмерного логарифма функции правдоподобия.
Рис.34
Получены величины : *земной* сигнал a= 1020 ед. АЦП и отраженный s =170 ед. АЦП. Таким образом, относительное различие амплитуд одноимённых сигналов для обоих вариантов обработки составляет единицы процентов. Это свидетельствует о непротиворечивости и однозначности использованных вариантов метода максимального правдоподобия.
Рис.35
Преимущество метода максимального правдоподобия заключается в том, что теоретически доказано, что получающиеся оценки оказываются асимптотически несмещёнными, нормально распределенными и асимптотически состоятельными.
По описанной методике был обработан ряд круглосуточных сеансов.[7]. Повторяемость суточной зависимости амплитуды отражённой волны иллюстрируется графиками на рис. 35, которые соответствуют результатам обработки данных методом максимального правдоподобия за трое последовательных суток ( 20.03 , 21.03 , 22.03.02 в 2002 году).
Резюмируя физический результат приведенных примеров, можно утверждать, что в весенний сезон ( март) на данной трассе на рабочей частоте 558кГц до 22-хчасов и после7-мичасов , т.е. в дневное время, отраженный сигнал отсутствовал. В ночное же время наблюдается четкий суточный ход амплитуды отраженного сигнала с максимумом примерно в полночь а, так как амплитуда этого сигнала распределена по закону Релея, то легко получить, что с вероятностью 90% она меняется от 0 до 3.25 от амплитуды *земного* сигнала.
Необходимо ещё раз подчеркнуть, что описанный метод определения относительной величины амплитуды отраженного от ионосферы сигнала исследован и работает только при условии, что амплитуда отраженного сигнала подчиняется принятому закону плотности распределения вероятности в средневолновом диапазоне радиоволн при наблюдении за сигналами, распространяющимися над сухопутными трассами, протяжённостью несколько сотен километров. При увеличении длины трассы возрастает роль отражений высоких кратностей, и характер распределения амплитуды становится иной.
Заметим также, что если бы ионосфера оказалась в таком «спокойном» состоянии, что отражения от неё имело бы зеркальный характер, то рассмотренный выше метод не работал бы: суммарная амплитуда принятого сигнала была бы константой, возможно подверженной лишь медленному «тренду» в течение суток . Однако в действительности механизм отражения электромагнитных волн не соответствует модели зеркального отражения и метод работает (!) с указанными выше ограничениями по диапазону и дальности.
В заключение можно сделать вывод, что изложенный метод определения относительных амплитуд (в обоих вариантах ) , основанный на анализе статистических характеристик суммарного сигнала, может служить удобным инструментом наблюдения вариаций отражающих свойств нижней ионосферы . Практическое удобство этого метода в том, что ,во-первых, имеется очень широкий набор *даровых* источников — вещательных станций, расположенных на различных расстояниях и излучающих разные частоты.Во-вторых, в том, что регистрирующая аппаратура достаточно проста и ею могут быть укомплектованы многие измерительные пункты. Это может обеспечить дополнительный канал мониторинга состояния нижней ионосферы.
Задачу оценки параметров сигнала рассмотрим на примере оценки амплитуды отраженного от ионосферы сигнала и его задержки по отношению к земному, не испытавшему отражения. Алгоритм, излагаемый ниже, целесообразно использовать, когда задержка отраженного радиоимпульса оказывается меньше, чем его длительность. На рис 5.1 приведён пример типичной картины временного положения импульсов радионавигационной системы Лоран-С, наблюдаемой на удалении около 700 км при распространении над морской трассой, Частота высокочастотного заполнения радиоимпульсов 100кГц, интервал между периодически излучаемыми импульсами равен 1мсек.
Рис.25
Видно, что первый отраженный от ионосферы сигнал частично наложен на земной.. Поэтому непосредственное определение как относительной его амплитуды, так и задержки оказывается невозможным. На временном интервале их наложения имеет место их векторное суммирование, разность же фаз высокочастотного заполнения неизвестна.
Построим функционал невязки априорно вычисленных модельных и экспериментально зарегистрированных данных.
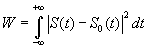
(5.1)
S(t)- принятый сигнал, So(t) — модель суммарного земного и отраженного сигналов. Функции описывающие априорно модели земног и отраженного сигналов считаем известными, они могут быть и различны.
Введем обозначения: X(t)- модельная функция земного сигнала, Y(t) — модельная функция отражённого сигнала, А и В- их амплитуды соответственно.
Модель принятого суммарного сигнала в местной шкале времени
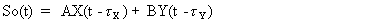
(5.2)

Тогда функционал невязки (5.1) запишется так:
W =
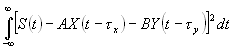
(5.3),
где обозначено:
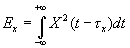
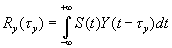
(5.3а)
В этих обозначениях имеем:
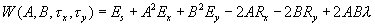
(5.4)
Используем метод наименьших квадратов. Уменьшим число искомых параметров, возьмем производные по А и по В и приравняем их нулю :
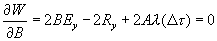
(5.5)
Отсюда найдём параметры А и В, выразив их через корреляционные функции (5.3).
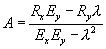
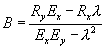
(5.6)
Таким образом, функционал невязки выразится через два неизвестных параметра tx и ty. :
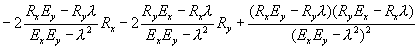
(5.7)
Далее эти два параметра tx , ty можно искать численным методом, применяя различные варианты метода спуска.
Практически нахождение этих параметров осложняется тем, что функционал невязки имеет ряд минимумов, а надо найти minimum minimorum. Функцию невязки W(tx, ty) можно наглядно представить как поверхность — рельеф над плоскостью искомых параметров t . Обратим внимание, что если сложение земного и отраженного сигналов происходит в противофазе, то функционал невязки имеет более резкие минимумы.
После того, как будут найдены значения tx* ,ty* в этих точках вычисляются все функции (5.3) и далее А и В (5.6). Тем самым будут определены все искомые параметры : временные положения земного tx и отраженного ty сигналов на временном отрезке наблюдения, а также отношение их амплитуд В/А.
Описанный выше алгоритм целесообразно реализовать в виде программы для ЭВМ . С помощью аналого-цифрового преобразователя (АЦП) преобразуем текущие значения принимаемого суммарного входного сигнала в цифровые отсчёты. Если непосредственно обрабатывать радиоимпульсы, то необходимо, по крайней мере, взять 10 отсчётов на периоде высокочастотного заполнения радиоимпульса. Но такое подробное описание сигнала оказывается излишним, если оценивать необходимый временной интервал оцифровки исходя из ширины спектра импульса по теореме Котельникова. (Dt = 0.5/fmax) , где fmax верхняя граница спектра сигнала. Приведенный в примере импульсный сигнал радионавигационной системы имеет спектр в полосе 100+30кГц. Более экономно можно оцифровать сигнал, если выделить квадратурные составляющие его огибающей, сместив его спектр в область низких частот (fmax= 30 кГц). В эксперименте получить квадратурные составляющие огибающей можно, применив схему с двумя фазовыми детекторами.
Рассмотрим вариант алгоритма «разделения» сигналов при использовании фазовых детекторов. Будем считать, что принятый сигнал F(t) сумма«земного» и однократно отраженного от ионосферы:
FS(t) = aX(t)sinwt + bY(t — tз)cosw(t — tз) = F(t)sin[wt + f(t)] (5.8)
Понятно, что на временном интервале, где имеет место суммирование «земного» и отраженного импульсов, фаза суммарного сигнала будет меняться по телу импульса, т.е f(t) есть функция времени. Здесь а ,b — масштабные множители амплитуд земного и отражённого сигналов — искомые параметры. X(t) ,Y(t) функции их огибающих, они считаются известными. Модельные сигналы следует выбирать подобными:
А(t) = А X(t — t1) sinw(t — t1 ) — модель земного,
B(t) = B Y(t — t2) sinw(t — t2) — модель отраженного.
Определению подлежат четыре параметра: А, В, t1, t2 . Для этого нужно минимизировать функционал невязки:
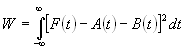
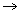
min (5.9)
Алгоритм минимизации нужно построить с учетом того, что принятый суммарный сигнал F(t) преобразуется на фазовых детекторах (ФД). В качестве управляющих сигналов на ФД подаются гармонические сигналы с частотой, равной частоте высокочастотного заполнения радиоимпульсов, фаза управляющего сигнала на одном ФД сдвинута относительно фазы другого на p/2. Принимаемый сигнал подаётся параллельно на оба фазовых детектора. Рис 27 .
Рис.27
На выходах низкочастотных фильтров фазовых детекторов получаются квадратурные составляющие принятого суммарного сигнала. Выпишем подробно функции квадратурных составляющих. Обозначив квадратурные составляющие опорных сигналов Аs , Аc , Вs , Вc , функционал (5.9) запишется так:
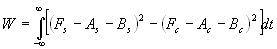
(5.10).
Далее функционал (5.10) представим так, чтобы искомые параметры А, В были выражены через t1 и t2 . Последние придётся искать численно. Запишем подынтегральную функцию в виде :
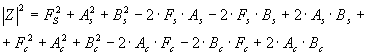
(5.11)
Величина 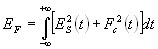 — описывает мощность сигнала, вычисляется по данным эксперимента. Учтём, что умножение модельного сигнала А (t) на управляющий гармонический в схемах ФД даёт:
— описывает мощность сигнала, вычисляется по данным эксперимента. Учтём, что умножение модельного сигнала А (t) на управляющий гармонический в схемах ФД даёт:
Аs(t) =
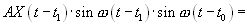
=
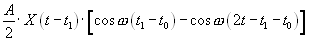
(5.12)
Ас =
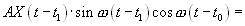
=
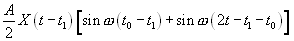
(5.13)
Замечая, что фильтры низких частот ФД значительно ослабляют сигналы на частоте 2w, далее соответствующие члены не будут учитываться. Поэтому приближённо имеем:
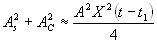
(5.14)
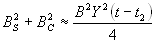

(5.15)
Преобразуем теперь суммы членов из выражения (5.11) так, чтобы искомые параметры A и В выделились коэффициентами:
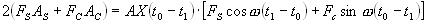
(5.16)

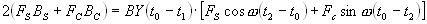
(5.17)
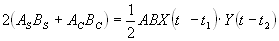
(5.18)
Примем следующие обозначения:
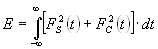 — энергия принятого сигнала,
— энергия принятого сигнала,
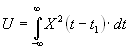 — энергия модельного земного сигнала,
— энергия модельного земного сигнала,
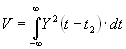 — энергия модельного отраженного сигнала (5.19)
— энергия модельного отраженного сигнала (5.19)
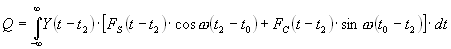
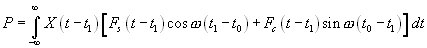
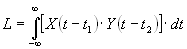 — взаимокорреляционная функция модельных сигналов.
— взаимокорреляционная функция модельных сигналов.
Возвращаясь к выражению (5.4) , которое можем теперь записать в виде:
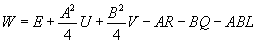
(5.20)
Аналогично тому, как это было сделано выше , [ см. (5.4 — 5.7)] , используем метод наименьших квадратов. Можно опять уменьшить количество неизвестных параметров, определяемых численно. Для этого продифференцируем функцию W по параметрам А , В и приравняем эти производные нулю. В результате масштабные множители А , В модельных земного и отраженного сигналов можно выразить через корреляционные функции (5.18) в виде:
Теперь функционал невязки неявно выражен как функция двух неизвестных параметров 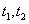 — временных положений земного и отраженного сигналов на временном интервале регистрации. Значения этих двух параметров, минимизирующих функционал невязки, приходится искать численными методами. Так же как и в рассмотренном выше варианте (без ФД), нахождение
— временных положений земного и отраженного сигналов на временном интервале регистрации. Значения этих двух параметров, минимизирующих функционал невязки, приходится искать численными методами. Так же как и в рассмотренном выше варианте (без ФД), нахождение 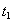 и
и 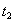 осложняется тем , что функционал невязки имеет ряд минимумов. Для отыскания главного целесообразно приблизительно определить положение огибающей суммарного сигнала на интервале регистрации. Кстати , следует отметить, что форма огибающей суммарного сигнала может существенно варьироваться. Она зависит от соотношения амплитуд суммируемых сигналов, а также от разности
осложняется тем , что функционал невязки имеет ряд минимумов. Для отыскания главного целесообразно приблизительно определить положение огибающей суммарного сигнала на интервале регистрации. Кстати , следует отметить, что форма огибающей суммарного сигнала может существенно варьироваться. Она зависит от соотношения амплитуд суммируемых сигналов, а также от разности 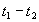 . На Рис. 28 в качестве иллюстрации приведены примеры огибающих суммарных сигналов для различных g = В/А и
. На Рис. 28 в качестве иллюстрации приведены примеры огибающих суммарных сигналов для различных g = В/А и 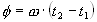 .
.
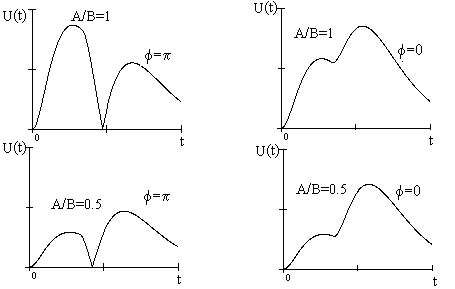
Однако ,несмотря, на значимые различия в форме суммарных огибающих при изменении D , могут быть предложены варианты оценки их положения на временной оси. Различия в форме огибающих суммарных сигналов приведены на рис. .
Конкретное описание таких алгоритмов в данном описании не приводится.
После того ,как численным методом минимизирован функционал невязки (5.20) , т. е. найдены 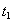 ,
, 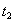 в этих точках вычисляются все функции (5.19 ) : E , U , V ,. R , Q , и L. Далее по (5.21) находятся масштабные множители А , В модельных функций земного и отраженного сигналов. Тем самым определено и искомое отношение амплитуд земного и отраженного сигналов:
в этих точках вычисляются все функции (5.19 ) : E , U , V ,. R , Q , и L. Далее по (5.21) находятся масштабные множители А , В модельных функций земного и отраженного сигналов. Тем самым определено и искомое отношение амплитуд земного и отраженного сигналов:
G =
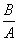
=
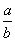
(5.22).
Очевидно, что описанный выше алгоритм целесообразно реализовать программно на ЭВМ, используя представление в цифровом виде как принятого суммарного , так и модельного сигналов. Принимаемый сигнал преобразуется в цифровую форму с помощью АЦП. Модельный же может сразу генерироваться в цифровой форме. Все описанные выше операции проводятся далее численно.
Таким образом, действующий приёмник может иметь в аналоговом варианте только входной полосовой фильтр и усилитель сигнала. После АЦП все операции выполняются над числами в соответствии с программой. В результате получаем оценки всех четырех искомых параметров A, B, 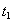 и
и 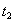 ,
, обеспечивающих минимум функционала невязки.
обеспечивающих минимум функционала невязки.
Выбор вариантов алгоритма разделения зависит от того, какого типа АЦП окажется предпочтительнее. Прямое преобразование требует более быстродействующих (и , следовательно, дорогих) АЦП , чем в варианте с ФД.
Здесь быстродействие АЦП оценивается просто по теореме Котельникова, исходя из ширины спектра принимаемого сигнала. Разрядность АЦП определит возможный выигрыш в отношении сигнал/ шум при накоплении.
В случае периодического сигнала целесообразно использовать его накопление в течении ряда периодов. Покажем, как может быть получен существенный выигрыш в отношении сигнал/шум на выходе фильтра. На периодическом сигнале этот выигрыш может быть реализован в статических свойствах сигнала и шума (который по прежнему будем считать«белым»). В частности, может быть использовано различие в корреляционных функциях детерминированного сигнала и шума. При этом мы рассмотрим последовательно два варианта построения «корреляционных фильтров». В первом — будем считать, что сигнал периодический, но период не известен;во-втором — период сигнала известен, но не известна его «фаза».
Рассмотрим первый вариант.
4.1 Выделение периодического сигнала из аддитивной его смеси с шумом, когда период не известен.
Используем алгоритм оценки корреляционной функции
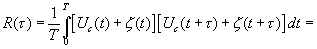
(4.1)
Здесь 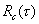 и
и 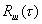 автокорреляционные функции сигнала и шума, а
автокорреляционные функции сигнала и шума, а 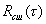 и
и 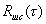 — взаимокорреляционные функции сигнала и шума. Так как сигнал и шум можно считать не зависимыми процессами, то взаимно корреляционные функции
— взаимокорреляционные функции сигнала и шума. Так как сигнал и шум можно считать не зависимыми процессами, то взаимно корреляционные функции 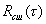 и
и 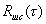 равны нулю.
равны нулю.
Оценим теперь 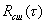 и .
и . 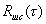 Будем считать, что на входе корреляционного фильтра включен аналоговый НЧ фильтр первого порядка (3.14). Тогда, в соответствии с (2.1), имеем
Будем считать, что на входе корреляционного фильтра включен аналоговый НЧ фильтр первого порядка (3.14). Тогда, в соответствии с (2.1), имеем
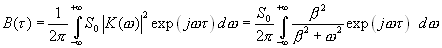
(4.2)
При вычислении интеграла будем различать два случая: 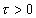 и
и 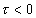 . Напомним, что
. Напомним, что 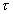 — задержка выборочных значений (сдвиг аргумента) второго сомножителя в подынтегральной функции (4.1). Знаменатель подынтегральной функции имеет два корня:
— задержка выборочных значений (сдвиг аргумента) второго сомножителя в подынтегральной функции (4.1). Знаменатель подынтегральной функции имеет два корня: 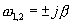 .
.
Вычисляя этот интеграл по формуле разложения [4,5], по вычетам, получаем с учетом знания 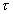 , явный вид:
, явный вид:
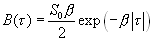
(4.3)
Полагая 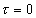 , получаем мощность шума на выходе:
, получаем мощность шума на выходе:
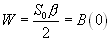
(4.4)
Напомним, что этот результат был получен и ранее ,формула (3.22).
Значение функции корреляции для периодического сигнала было приведено выше (1.14). Учитывая его, получаем значение искомой корреляционной функции:
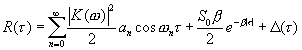
(4.5)
Член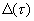 имеет смысл «шума», обусловлен величиной суммы
имеет смысл «шума», обусловлен величиной суммы 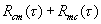 при конечном времени интегрирования и усреднения ,стремится к нулю при увеличении T и t. Обращаясь к (4.5) видим, что при увеличении сдвига-задержки
при конечном времени интегрирования и усреднения ,стремится к нулю при увеличении T и t. Обращаясь к (4.5) видим, что при увеличении сдвига-задержки 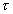 первое слагаемое (сумма) описывает неубывающую осциллирующую функцию, полезный сигнал по аргументу
первое слагаемое (сумма) описывает неубывающую осциллирующую функцию, полезный сигнал по аргументу 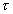 ( а не t) , второе — экспоненциально убывает. Таким образом обеспечивается принципиальная возможность выделить осциллирующий член — полезный сигнал из аддитивной смеси сигнала и шума, имеющейся на входе фильтра. Следует обратить внимание, что для реализации рассмотренного способа необходимо на каждом шаге изменения
( а не t) , второе — экспоненциально убывает. Таким образом обеспечивается принципиальная возможность выделить осциллирующий член — полезный сигнал из аддитивной смеси сигнала и шума, имеющейся на входе фильтра. Следует обратить внимание, что для реализации рассмотренного способа необходимо на каждом шаге изменения 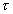 вычислять соответствующие интегралы по интервалу Т, чтобы обеспечить малую величину приближенных величин взаимокорреляционных функций
вычислять соответствующие интегралы по интервалу Т, чтобы обеспечить малую величину приближенных величин взаимокорреляционных функций 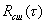 и
и 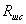 . (см. рис. 10)
. (см. рис. 10)
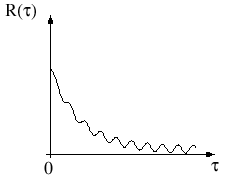
Рис. 10
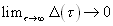
. (4.6).
Конечная величина интервала интегрирования приводит к тому, что величина D (t) 0 будет «шумом».Величину такого рода «шума» достаточно просто оценить для случая, когда период полезного сигнала известен.
4.2 Выделение гармонического сигнала из шума, когда его период известен.
Рассмотрим теперь случай, когда период полезного сигнала известен, но неизвестна его «фаза», да и само наличие под вопросом. В этом варианте целесообразно использовать алгоритм вычисления взаимокорреляционной функции аддитивной смеси полезного сигнала и шума и опорным сигналом , период которого равен периоду полезного сигнала. Возможный выигрыш в отношении сигнал/шум рассмотрим на примере гармонического сигнала. Опорный сигнал тоже положим гармоническим, но с другой амплитудой и фазой. Шум будем считать «белым».
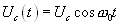
;
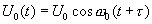
(4.7)
Таким образом искомая взаимокорреляционная функция будет
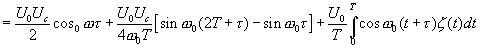
(4.8)
Второй член в (4.8) можно рассматривать, как фон при конечном времени интегрирования, тогда, как третий интеграл имеет смысл «шума».
И «фон» и «шум» убывают при увеличении времени интегрирования Т. Очевидно, что «фон» убывает как 1/Т. Характер убывания «шума» при увеличении Т рассмотрим более подробно, отдельно.
Для оценки величины «шума» используем соотношение Хинчина [12]:
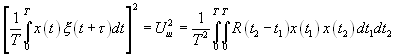
(4.9).
Здесь 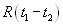 — корреляционная функция случайного процесса, x(t)- детерминированная функция. Примем условия рассмотренного выше примера: шум на входе будем полагать «белым» со спектральной плотностью мощности
— корреляционная функция случайного процесса, x(t)- детерминированная функция. Примем условия рассмотренного выше примера: шум на входе будем полагать «белым» со спектральной плотностью мощности 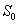 , на входе корреляционного фильтра включен RC фильтр с коэффициентом передачи.
, на входе корреляционного фильтра включен RC фильтр с коэффициентом передачи.
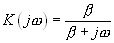
.
Выше было показано, что корреляционная функция случайного процесса на выходе такого RC фильтре имеет вид:
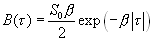
(4.3)
Подставляя эти функции в (4.9) и вычисляя двойной интеграл, получаем громоздкое выражение ( см.приложение), включающее члены, имеющие различное убывание при увеличении интервала интегрирования Т.
Если учесть только наиболее медленно убывающий член 1/T, то приближенно получаем:
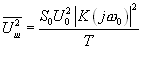
(4.10).
Эта формула и описывает мощность «шума» на выходе корреляционного фильтра, обусловленного конечным временем интегрирования Т. «Амплитуда шума» соответственно:
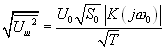
(4.11).
Заметим, что роль частотного интервала здесь играет величина 1/T Величина же 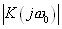 просто безрамерный коэффициент.
просто безрамерный коэффициент.
Обращаясь к (4.8), напомним, что первый член описывает взаимокорреляционную функцию детерминированных сигналов, полезного 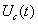 и опорного
и опорного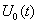 и, следовательно, имеет смысл полезного сигнала на выходе корреляционного фильтра:
и, следовательно, имеет смысл полезного сигнала на выходе корреляционного фильтра:
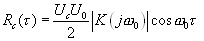
(4.12).
Очевидно, что отношение сигнал/шум, (предполагая , что 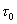 выбирается так,чтобы
выбирается так,чтобы 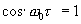 ), будет:
), будет:
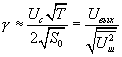
(4.13).
Это важный результат: при накоплении периодического сигнала, которое можно вести на протяжении ряда периодов, отношение амплитуд сигнал/шум на выходе корреляционного фильтра увеличивается пропорционально корню квадратному от времени интегрирования. (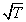 ). Понятно, что полученная зависимость сигнал/шум от времени интегрирования (как
). Понятно, что полученная зависимость сигнал/шум от времени интегрирования (как 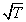 ) сохранится и в случае сложного периодического ( импульсного) сигнала. Заметим, что в этом случае и опорный сигнал должен иметь спектр такой же, как и спектр полезного сигнала.
) сохранится и в случае сложного периодического ( импульсного) сигнала. Заметим, что в этом случае и опорный сигнал должен иметь спектр такой же, как и спектр полезного сигнала.
Реализовать описанный алгоритм возможно используя преобразование суммарного входного сигнала в цифровую форму , что позволит далее производить все операции вычисления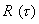 с помощью программ на ЭВМ. При необходимости иметь выходной сигнал в аналоговой форме нужно использовать цифроаналоговый преобразователь. Кроме того, для ограничения спектра шума по входу необходимо сохранить, аналоговый фильтр, подобный рассмотренному в данном примере
с помощью программ на ЭВМ. При необходимости иметь выходной сигнал в аналоговой форме нужно использовать цифроаналоговый преобразователь. Кроме того, для ограничения спектра шума по входу необходимо сохранить, аналоговый фильтр, подобный рассмотренному в данном примере 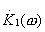 .
.
В заключение этого раздела отметим, что результат здесь был получен на «временном языке», т. е. отношение сигнал/шум на выходе корреляционного фильтра, выражено как функция времени накопления (интегрирования). Но при этом пока неочевидно каков будет коэффициент передачи корреляционного фильтра в частотной области.
Ответ на этот вопрос удобно получить, рассмотрев аналоговый вариант корреляционного фильтра.
4.3 Аналоговый вариант корреляционного фильтра.
В радиотехнических терминах такой корреляционный фильтр реализуется схемой фазового детектора. Действительно, функционально схема фазового детектора реализует алгоритм определения взаимной корреляционной функции.
Рис. 11
Эта схема содержит входной фильтр 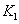 , генератор опорного сигнала, перемножитель входного сигнала с опорным и накопитель- инерционный узкополосный фильтр
, генератор опорного сигнала, перемножитель входного сигнала с опорным и накопитель- инерционный узкополосный фильтр 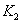 , выполняющий приближенно операцию интегрирования.
, выполняющий приближенно операцию интегрирования.
Рассмотрим функционирование этой схемы, обращая внимание на преобразование спектра принимаемого (входного) сигнала.
Полезный сигнал опять будем считать гармоническим, а входной сигнал аддитивной смесью этого сигнала с «белым» шумом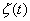 .
.
Пусть 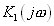 есть резонансный RLC фильтр
есть резонансный RLC фильтр
Рис.12
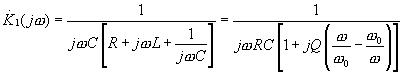
(4.14)
будем считать 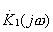 узкополосным, тогда при выполнении условия
узкополосным, тогда при выполнении условия 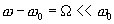 получим приближенное выражение:
получим приближенное выражение:
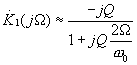
,
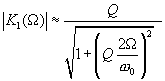
(4.15)
Удобно ввести ширину полосы пропускания фильтра 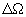 при заданной неравномерности
при заданной неравномерности 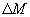 , примем
, примем 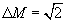 . Тогда
. Тогда 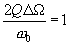 ,
, 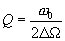 -добротность, следовательно,
-добротность, следовательно,
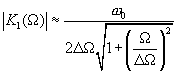
(4.16)
Заметим, что на резонансной частоте 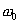 имеем
имеем 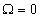 и
и 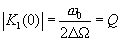
Будем далее учитывать нормированный модуль коэффициента передачи входного фильтра
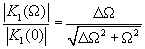
(4.17)
Рассмотрим прохождение белого шума через такой резонансный фильтр 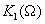 , считая, что его спектральная плотность мощности-
, считая, что его спектральная плотность мощности-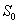 .
.
Используя (2.3) , имеем выражение для спектральной плотности мощности шума на выходе резонансного фильтра 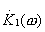 , на входе перемножителя.
, на входе перемножителя.
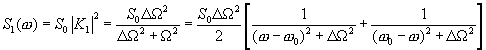
(4.18)
В качестве второго сомножителя на перемножитель подается гармонический сигнал. Здесь возможны два варианта: первый — частота опорного сигнала равна частоте полезного сигнала (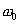 ). В этом случае фильтр
). В этом случае фильтр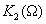 должен быть фильтром НЧ. Полезный выходной сигнал будет представлен постоянной составляющей. Второй вариант- частота опорного сигнала
должен быть фильтром НЧ. Полезный выходной сигнал будет представлен постоянной составляющей. Второй вариант- частота опорного сигнала 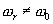 . Здесь выходной фильтр
. Здесь выходной фильтр 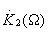 должен быть резонансным на частоте
должен быть резонансным на частоте 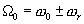 .
.
Рассмотрим первый вариант: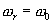 , опорный гармонический сигнал
, опорный гармонический сигнал
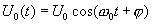
(4.19)
Его спектр
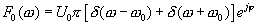
(4.20)
Убедимся, что спектр (4.20) связан преобразованием Фурье с (4.19)

(4.21)
Здесь использовано известное свойство d (x) функции :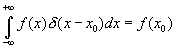 .
.
Итак, имеем спектры сомножителей, хотим найти спектр произведения — спектр на входе перемножителя. Используем формулу свертки в частотной области [8 ]:
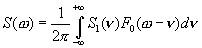
(4.22)
Спектры сомножителей (4.19) и (4.20) изображены на рис.13
рис.13
Подставив значения спектральных функций (4.18) и (4.20) в (4.22) , получим спектральную плотность мощности шума на выходе перемножителя:
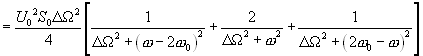
(4.23)
Наконец, спектральная плотность мощности шума на выходе узкополосного НЧ фильтра 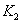 будет содержать только полосу спектра вблизи
будет содержать только полосу спектра вблизи 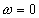 . Это дает:
. Это дает:
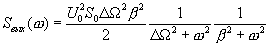
(4.24)
Теперь легко найти мощность шума, имеющую такой спектр. Это удобно сделать так:
найти автокорреляционную функцию, соответствующую этому спектру и устремить t -> 0
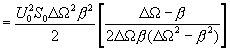
(4.25)
Полоса фильтра 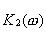 выбирается много меньше, чем у фильтра
выбирается много меньше, чем у фильтра 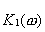 , то есть
, то есть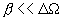 , при этом (4.25) приблизительно дает:
, при этом (4.25) приблизительно дает:
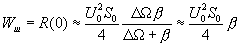
(4.26)
Таким образом, мощность шума на выходе фазового детектора -корреляционного фильтра пропорциональна узкой полосе выходного фильтра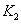 равной DW
равной DW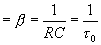 Аналогично оценим величину и мощность полезного сигнала. Функция взаимной корреляции полезного гармонического сигнала была определена ранее (4.8),(4.12). Она описывает величину выходного полезного сигнала, в данном случае величину постоянной составляющей как функции задержки опорного сигнала
Аналогично оценим величину и мощность полезного сигнала. Функция взаимной корреляции полезного гармонического сигнала была определена ранее (4.8),(4.12). Она описывает величину выходного полезного сигнала, в данном случае величину постоянной составляющей как функции задержки опорного сигнала 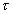 .
.
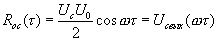
(4.12)
Максимум сигнала на выходе фазового детектора получается при значениях
где n- целое число. Следует обратить внимание, что формула (4.12) описывает не мощность сигнала 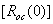 , а его величину («амплитуду»). Множителю
, а его величину («амплитуду»). Множителю 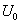 следует придать смысл коэффициента усиления. Этот множитель присутствует и в выражении, оценивающем мощность шума. (
следует придать смысл коэффициента усиления. Этот множитель присутствует и в выражении, оценивающем мощность шума. (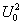 ). Поэтому мощность сигнала ( его максимального значения при
). Поэтому мощность сигнала ( его максимального значения при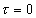 ) будет описываться так
) будет описываться так
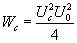
(4.27)
А отношение сигнал/шум по мощности (см 4.26) есть:
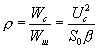
(4.28)
соответственно, отношения сигнал/шум по амплитуде на выходе корреляционного фильтра — фазового детектора будет
4.4. Супергетеродинный приёмник — аналоговый корреляционный фильтр
Коротко рассмотрим отмеченный выше второй вариант: частота опорного генератора отлична от частоты полезного сигнала 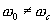 здесь после перемножения полезного сигнала с опорным получим сумму двух гармонических сигналов на суммарной и разностной частотах
здесь после перемножения полезного сигнала с опорным получим сумму двух гармонических сигналов на суммарной и разностной частотах
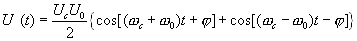
(4.30)
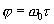 -фаза опорного сигнала. Здесь сомножителями участвовали сигналы:
-фаза опорного сигнала. Здесь сомножителями участвовали сигналы:
,
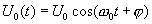
.
В качестве узкополосного интегрирующего фильтра в этом случае нужно использовать резонансный фильтр — ( усилитель), настроенный на суммарную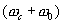 или разностною
или разностною 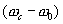 частоту. Отличием от рассмотренного выше варианта является то , что при изменении фазы опорного сигнала относительно фазы входного (полезного) сигнала амплитуда гармонического сигнала на разностной и суммарной частоте будет оставаться постоянной. Изменяться будет только фаза сигнала на этих частотах. Функционально схема, изображенная на рис.11 ., включающая . в качестве фильтра К2 резонансный фильтр, настроенный на
частоту. Отличием от рассмотренного выше варианта является то , что при изменении фазы опорного сигнала относительно фазы входного (полезного) сигнала амплитуда гармонического сигнала на разностной и суммарной частоте будет оставаться постоянной. Изменяться будет только фаза сигнала на этих частотах. Функционально схема, изображенная на рис.11 ., включающая . в качестве фильтра К2 резонансный фильтр, настроенный на 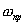 , является типовой схемой супергетеродинного приёмника в высокочастотной её части и работает как аналоговый корреляционный фильтр. Преобразование шума в этом варианте фильтра легко оценить совершенно также, как это было сделано выше, только размещение полос спектра шума по диапазону будет другим.
, является типовой схемой супергетеродинного приёмника в высокочастотной её части и работает как аналоговый корреляционный фильтр. Преобразование шума в этом варианте фильтра легко оценить совершенно также, как это было сделано выше, только размещение полос спектра шума по диапазону будет другим.
рис.14
Не повторяя очевидных выкладок качественно поясним это рисунком (Рис.14), на котором по осям частот указаны частоты сигналов и полосы спектра шума. Соотношение сигнал/шум и в этом случае будут также определятся выражениями (4.28) и (4.29):
Формула (4.28) дает ответ и на вопрос об оптимальном комплексном коэффициенте передачи корреляционного фильтра. Для гармонического сигнала — это коэффициент 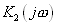 , описывающий узкополосный выходной (интегрирующий) фильтр. В случае, когда частота опорного сигнала совпадает с частотой полезного это будет низкочастотный фильтр.(3.16) или (3.32). Если частота опорного отлична от частоты сигнала — это будет резонансный фильтр(4.15), настроенный на суммарную или разностную частоту
, описывающий узкополосный выходной (интегрирующий) фильтр. В случае, когда частота опорного сигнала совпадает с частотой полезного это будет низкочастотный фильтр.(3.16) или (3.32). Если частота опорного отлична от частоты сигнала — это будет резонансный фильтр(4.15), настроенный на суммарную или разностную частоту 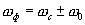 . В этом случае целесообразно совместить функцию фильтрации с усилением, т.е. в качестве интегрирующего элемента использовать резонансный усилитель. Однако на отношение сигнал/шум величина этого усиления влиять не будет: и шум и сигнал усиливаются одинаково.
. В этом случае целесообразно совместить функцию фильтрации с усилением, т.е. в качестве интегрирующего элемента использовать резонансный усилитель. Однако на отношение сигнал/шум величина этого усиления влиять не будет: и шум и сигнал усиливаются одинаково.
Отметим, что рассмотренные выше примеры, когда в качестве полезного сигнала рассматривается неограниченный во времени гармонический сигнал не представляет непосредственного интереса: здесь время накопления формально может стремиться к бесконечности, а полоса пропускания фильтра к нулю. (Время установления сигнала в таком фильтре будет стремиться к бесконечности).
Однако полученные результаты являются основой для оценки отношения сигнал/шум при ограниченном времени интегрирования или конечной полосе фильтра. Уместно напомнить, что полоса фильтра 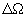 и время установления
и время установления 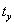 связаны соотношением :
связаны соотношением : 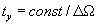 .
.
Так, например, задавшись временем наблюдения, ( можно приравнять его времени установления в наиболее узкополосном звене), получаем необходимую ширину полосы узкополосного фильтра (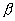 ). А при заданных величинах входного сигнала
). А при заданных величинах входного сигнала 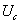 и спектральной плотности мощности шума
и спектральной плотности мощности шума 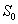 , определяем и отношение сигнал/шум на выходе. Наоборот, задавшись желаемым соотношением сигнал/шум на выходе ( при известных данных входных
, определяем и отношение сигнал/шум на выходе. Наоборот, задавшись желаемым соотношением сигнал/шум на выходе ( при известных данных входных 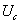 и
и 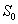 ), получаем величину требуемого времени установления (наблюдения) или полосу интегрирующего узкополосного фильтра. Оценка отношения сигнал / шум будет продолжена при рассмотрении конкретной схемы оптимального фильтра в разделе 4.5.2
), получаем величину требуемого времени установления (наблюдения) или полосу интегрирующего узкополосного фильтра. Оценка отношения сигнал / шум будет продолжена при рассмотрении конкретной схемы оптимального фильтра в разделе 4.5.2
4.5 Оптимальный прием сложного периодического сигнала
Гораздо более интересным является случай, когда полезный сигнал является сложным периодическим сигналом. Для такого сигнала будут рассмотрены два вопроса:
-
Какой вид будет иметь взаимно-корреляционная функция, как функция временного сдвига опорного сигнала относительно входного, полезного?
-
Какова будет АЧХ оптимального фильтра для сложного (импульсного) периодического сигнала и как будет зависеть отношение сигнал/шум от параметров фильтра?
Получив ответы на эти вопросы, окажется возможным оценить выигрыш в отношении сигнал/шум при ограниченном времени наблюдения. Например, при приеме 'пачки' из n импульсов на заданном временном интервале.
Отдельно надо будет оценить необходимую разрядность аналого-цифрового преобразователя, способного реализовать требуемый выигрыш в отношении сигнал/шум.
4.5.1 Периодическая последовательность прямоугольных импульсов
В качестве первого примера рассмотрим выделение полезного сигнала 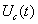 , представляющего периодическую последовательность прямоугольных импульсов, которая принимается на фоне шума
, представляющего периодическую последовательность прямоугольных импульсов, которая принимается на фоне шума 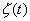 .
.
В роли приемного устройства, обеспечивающего желаемый выигрыш в отношении сигнал/шум, будем использовать корреляционный аналоговый фильтр, описанный выше. В качестве опорного сигнала будет использоваться аналогичная периодическая последовательность прямоугольных импульсов с той же частотой повторения, но, возможно другой длительности. Работу перемножителя в данном случае можно представлять как действие ключа: во время опорного импульса ключ замкнут, в его отсутствии — разомкнут. Коэффициент передачи перемножающего устройства периодически изменяется от единицы до нуля.
Рис 15
Для нахождения 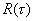 , как и ранее, используем соотношение Фурье (2.1), найдя сначала соответствующую спектральную функцию
, как и ранее, используем соотношение Фурье (2.1), найдя сначала соответствующую спектральную функцию 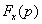 . Для этого можно вначале определить спектр произведения одиночных импульсов, а затем, используя известную связь спектра одиночного и периодического сигналов, найти искомый спектр произведения периодических сигналов.
. Для этого можно вначале определить спектр произведения одиночных импульсов, а затем, используя известную связь спектра одиночного и периодического сигналов, найти искомый спектр произведения периодических сигналов.
Принятые обозначения параметров импульсов изображены на рисунке
Изображения этих одиночных импульсов будут соответственно
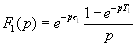
,
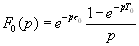
(4.31)
Изображение произведения временных функций определим, используя формулу свертки в частной области
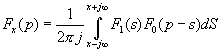
(4.32)
Заметим, что при интегрировании (4.32) точку Х на вещественной оси и комплексную точку Р следует взять настолько далеко вправо, чтобы для точки S, перемещающейся по прямой интегрирования (от 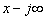 до
до 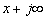 ) соблюдались два условия: во-первых, чтобы S оставалось в полуплоскости сходимости изображения
) соблюдались два условия: во-первых, чтобы S оставалось в полуплоскости сходимости изображения 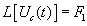 , и во-вторых, чтобы P-S оставалось в полуплоскости изображения
, и во-вторых, чтобы P-S оставалось в полуплоскости изображения 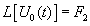 [ Дёч ]
[ Дёч ]
Подставляя (4.31) в (4.32) получаем, что необходимо вычислить четыре интеграла
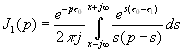
,
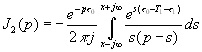
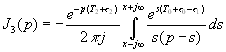
,
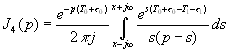
(4.33)
Значения этих интегралов зависят от знака показателя экспоненты. Покажем, как он влияет на примере вычисления 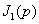 , используя формулу разложения [ ], [ ], т. е. считая его по вычетам. Знаменатель в (4.33) имеет два корня S=0 и S=P , второй корень следует считать расположенным правее исходного контура интегрирования, (в правой полуплоскости S). При
, используя формулу разложения [ ], [ ], т. е. считая его по вычетам. Знаменатель в (4.33) имеет два корня S=0 и S=P , второй корень следует считать расположенным правее исходного контура интегрирования, (в правой полуплоскости S). При 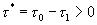 , в соответствии с леммой Жордана, можем исходный контур замкнуть полуокружностью бесконечно большого радиуса в левой полуплоскости S. При этом в образовавшемся замкнутом контуре
, в соответствии с леммой Жордана, можем исходный контур замкнуть полуокружностью бесконечно большого радиуса в левой полуплоскости S. При этом в образовавшемся замкнутом контуре 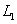 окажется только полюс в точке S=0. Что дает:
окажется только полюс в точке S=0. Что дает:
Если же 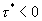 , то лемма Жордана позволяет замкнуть исходный контур полуокружностью в правой полуплоскости S, теперь в замкнутом контуре окажется полюс S=P. Вычисляя этот вычет (с учетом знака (-)из-за изменения направления обхода по замкнутому контуру L), получаем:
, то лемма Жордана позволяет замкнуть исходный контур полуокружностью в правой полуплоскости S, теперь в замкнутом контуре окажется полюс S=P. Вычисляя этот вычет (с учетом знака (-)из-за изменения направления обхода по замкнутому контуру L), получаем:
Аналогично вычисляются и остальные интегралы (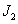 ,
,
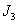 и
и 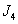 ).
).
Результаты вычисления представлены в таблице 1.
Очевидно, что искомое изображение 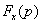 (4.32) на выходе перемножителя-ключа получается суммированием
(4.32) на выходе перемножителя-ключа получается суммированием 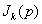 с учетом взаимного положения
с учетом взаимного положения 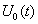 и
и 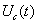 во времени. Наглядно этот результат представлен на рисунке (в случаях B,C,D,E не выписаны сокращающиеся слагаемые).
во времени. Наглядно этот результат представлен на рисунке (в случаях B,C,D,E не выписаны сокращающиеся слагаемые).
Приведенные данные позволяют построить и функцию взаимной корреляции на выходе узкополосного, интегрирующего звена 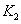 , выделяющего (в данном примере) постоянную составляющую, величина которой зависит от взаимного положения импульсов во времени. Учитывая, что при изменении сдвига-задержки
, выделяющего (в данном примере) постоянную составляющую, величина которой зависит от взаимного положения импульсов во времени. Учитывая, что при изменении сдвига-задержки 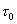 опорного сигнала на входе звена
опорного сигнала на входе звена 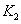 меняется длительность импульса
меняется длительность импульса 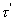 и учитывая, что постоянная составляющая в спектре пропорциональна
и учитывая, что постоянная составляющая в спектре пропорциональна 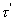 , имеем:
, имеем:

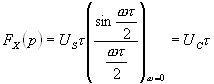
(4.35)
Получаем, что при изменении временного положения опорного импульса относительно сигнала 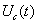 взаимокорреляционная функция
взаимокорреляционная функция 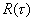 будет иметь вид или трапеции (при
будет иметь вид или трапеции (при 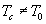 ), или видтреугольника (
), или видтреугольника (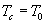 ) (см. рис.17). Теперь перейдем к анализу процессов в описанном фильтре при приеме периодической последовательн
) (см. рис.17). Теперь перейдем к анализу процессов в описанном фильтре при приеме периодической последовательн
ости импульсов. Проведем рассмотрение со спектральной точки зрения. Используем известную связь между спектральной плотностью 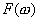 одиночного импульса и дискретным спектром периодической последовательности таких импульсов, который описывается рядом Фурье. Связь такова:
одиночного импульса и дискретным спектром периодической последовательности таких импульсов, который описывается рядом Фурье. Связь такова:
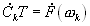
и
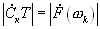
(4.36),
где 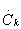 — комплексная амплитуда катой гармоники спектра периодической последовательности, T- период следования импульсов,
— комплексная амплитуда катой гармоники спектра периодической последовательности, T- период следования импульсов, 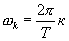 .
.
Из формулы следует, что амплитуды гармоник периодической последовательности, умноженные на период Т, равны значениям функции модуля спектра одиночного импульса на частотах 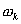 .
.
Для обеспечения оптимального приема периодической последовательности используем опорный сигнал также представляющий периодическую последовательность импульсов с тем же периодом. Таким образом, спектр опорного сигнала будет также дискретным; его гармоники будут иметь те же частоты , что и гармоники спектра входного сигнала.
Каков же будет спектр на выходе умножителя?
Каждая гармоника спектра опорного сигнала в результате перемножения дает суммарную и разностную частоту со всеми гармониками спектра сигнала. Если далее включен фильтр НЧ (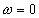 ) с полосой более узкой, чем дистанция между гармониками спектров (
) с полосой более узкой, чем дистанция между гармониками спектров (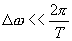 ), то будет выделена сумма постоянных составляющих, получающихся в результате перемножения гармоник спектров на совпадающих частотах. Все остальные комбинационные частоты не будут пропущены таким узкополосным фильтром. Следовательно, суммарный сигнал (как сумма постоянных составляющих) в результате перемножения и фильтрации одинаковых гармоник спектров входного и опорного сигналов будет
), то будет выделена сумма постоянных составляющих, получающихся в результате перемножения гармоник спектров на совпадающих частотах. Все остальные комбинационные частоты не будут пропущены таким узкополосным фильтром. Следовательно, суммарный сигнал (как сумма постоянных составляющих) в результате перемножения и фильтрации одинаковых гармоник спектров входного и опорного сигналов будет
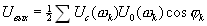
(4.37),
Сравнивая (4.37) с (1.14), видим, что данная сумма описывает взаимокорреляционную функцию периодических сигналов, имеющих одинаковые периоды Т.
Заметим, что данная взаимокорреляционная функция будет описывать периодическое повторение (по переменной t ) полученной выше корреляционной функции для одиночных сигналов (4.34).
Какова же будет амплитудно-частотная характеристика такого фильтра?
В результате простого модельного эксперимента убеждаемся, что рассматриваемый фильтр будет иметь гребенчатую амплитудно-частотную (АЧХ) характеристику. Действительно, представим, что для определения АЧХ подаем на вход испытательный гармонический сигнал 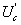 с медленно изменяющейся во времени частотой. Так медленно изменяющейся, чтобы успевал устанавливаться переходной процесс в узкополосном усилителе. При этом обеспечим, что ширина полосы пропускания НЧ фильтра будет много меньше, чем частотный интервал между гармониками в спектре опорного периодического импульсного сигнала. Очевидно, что всякий раз, когда разность частоты какой либо гармоники спектра опорного сигнала и изменяющейся частоты испытательного сигнала оказывается в полосе пропускания НЧ фильтра, на его выходе появляется сигнал. Изменение амплитуды этого сигнала во времени приближенно описывает АЧХ этого низкочастотного фильтра. И так будет всякий раз при прохождении изменяющейся частоты испытательного сигнала
с медленно изменяющейся во времени частотой. Так медленно изменяющейся, чтобы успевал устанавливаться переходной процесс в узкополосном усилителе. При этом обеспечим, что ширина полосы пропускания НЧ фильтра будет много меньше, чем частотный интервал между гармониками в спектре опорного периодического импульсного сигнала. Очевидно, что всякий раз, когда разность частоты какой либо гармоники спектра опорного сигнала и изменяющейся частоты испытательного сигнала оказывается в полосе пропускания НЧ фильтра, на его выходе появляется сигнал. Изменение амплитуды этого сигнала во времени приближенно описывает АЧХ этого низкочастотного фильтра. И так будет всякий раз при прохождении изменяющейся частоты испытательного сигнала 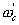 по интервалам
по интервалам 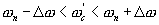 , где
, где 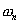 - частоты гармоник спектра (
- частоты гармоник спектра (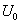 ) опорного сигнала. Таким образом, в целом полученная АЧХ будет иметь вид «гребенки». Максимумы зубцов этой гребенки будут лежать на частотах
) опорного сигнала. Таким образом, в целом полученная АЧХ будет иметь вид «гребенки». Максимумы зубцов этой гребенки будут лежать на частотах 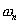 , ширина же и форма каждого зубца определяются АЧХ узкополосного фильтра, интервалы между зубцами равны интервалам, между гармониками
, ширина же и форма каждого зубца определяются АЧХ узкополосного фильтра, интервалы между зубцами равны интервалам, между гармониками 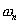 опорного сигнала.
опорного сигнала.
4.5.2 Оптимальный фильтр для периодической последовательности радиоимпульсов
Особенно явно преимущества корреляционного фильтра, использующего импульсный опорный сигнал, проявятся при приеме радиоимпульсов с высокочастотным заполнением. В этом случае в качестве узкополосного элемента целесообразно использовать резонансный усилитель, обеспечивающий и необходимое усиление сигнала. В этом варианте корреляционный фильтр — это известный супергетеродинный приемник, но с импульсным гетеродином и достаточно узкополосным усилителем промежуточной частоты.
Легко убедиться, что если опорный, (гетеродинный) сигнал это радиоимпульс с несущей частотой 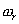 и частотой повторения
и частотой повторения 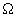 , то данный приемник-фильтр будет иметь гребенчатую характеристику.
, то данный приемник-фильтр будет иметь гребенчатую характеристику.
Действительно, будем снимать АЧХ устройства, опять подавая на вход смесителя испытательный гармонический сигнал 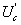 с медленно изменяющейся частотой. При этом будем использовать импульсный гетеродин и обеспечим, что ширина полосы пропускания резонансного усилителя будет много меньше, чем частотный интервал между гармониками в спектре опорного сигнала — гетеродина
с медленно изменяющейся частотой. При этом будем использовать импульсный гетеродин и обеспечим, что ширина полосы пропускания резонансного усилителя будет много меньше, чем частотный интервал между гармониками в спектре опорного сигнала — гетеродина 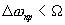 . Тогда всякий раз, когда разность (или сумма) текущей частоты испытательного сигнала
. Тогда всякий раз, когда разность (или сумма) текущей частоты испытательного сигнала 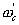 с некоторой гармоникой гетеродина оказывается равной
с некоторой гармоникой гетеродина оказывается равной 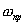 (в пределах полосы
(в пределах полосы 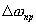 ) сигнал проходит через узкополосный усилитель. Это будет гармонический сигнал промежуточной частоты с частотой
) сигнал проходит через узкополосный усилитель. Это будет гармонический сигнал промежуточной частоты с частотой 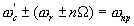 . И так будет повторяться каждый раз, когда разность или сумма частот испытательного сигнала и какой либо изгармоник (n) гетеродина равны
. И так будет повторяться каждый раз, когда разность или сумма частот испытательного сигнала и какой либо изгармоник (n) гетеродина равны 
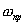 . Таким образом, очевидно, что амплитудно-частотная характеристика приемника-фильтра будет иметь вид «гребенки». Ширина и форма «зубца» определяется частотной характеристикой узкополосного резонансного усилителя, а положение «зубцов» на шкале частот — положением гармоник гетеродина и номиналом
. Таким образом, очевидно, что амплитудно-частотная характеристика приемника-фильтра будет иметь вид «гребенки». Ширина и форма «зубца» определяется частотной характеристикой узкополосного резонансного усилителя, а положение «зубцов» на шкале частот — положением гармоник гетеродина и номиналом 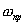 . Теперь рассмотрим процесс в приемнике-фильтре при включении на его вход периодической последовательности радиоимпульсов. Анализ будем проводить с двух точек зрения: временной и спектральной.
. Теперь рассмотрим процесс в приемнике-фильтре при включении на его вход периодической последовательности радиоимпульсов. Анализ будем проводить с двух точек зрения: временной и спектральной.
Начнем с временной. Предположим, что последовательность импульсов опорного сигнала-гетеродина медленно смещается относительно последовательности входных радиоимпульсов. Такое предположение означает, что частоты повторения импульсов в этих последовательностях отличаются, но так что бы 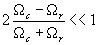 .
.
На рисунке 19 изображены три относительных положений импульсов во времени.
рис.19
Импульсы частично перекрываются во времени, импульсы совпадают, импульсы разнесены. Очевидно, что во втором случае сигнал промежуточной частоты будет иметь максимальное значение, при разносе их во времени 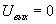 , а при частичном перекрытии (||) выходной сигнал будет иметь отличное от нуля значение, но
, а при частичном перекрытии (||) выходной сигнал будет иметь отличное от нуля значение, но 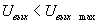 . Зависимость амплитуды гармонического сигнала промежуточной частоты от величины их «задержки»
. Зависимость амплитуды гармонического сигнала промежуточной частоты от величины их «задержки» 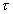 — относительного положения во времени будет описываться корреляционной функцией, как это было показано выше для одиночных сигналов. Только теперь эта корреляционная функция будет периодической функцией
— относительного положения во времени будет описываться корреляционной функцией, как это было показано выше для одиночных сигналов. Только теперь эта корреляционная функция будет периодической функцией 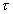 с периодом Т.
с периодом Т.
рис.20
Рассмотрим теперь этот процесс с частотной, спектральной точки зрения. Так как оба сигнала, и входящий, и опорный являются радиоимпульсами с различной несущей (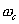 ), но с одинаковыми частотами повторения
), но с одинаковыми частотами повторения 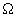 , то каждому соответствует линейчатый (дискретный) спектр с некоторой эффективной шириной. Их спектры разнесены по шкале частот на номинал промежуточной частоты.
, то каждому соответствует линейчатый (дискретный) спектр с некоторой эффективной шириной. Их спектры разнесены по шкале частот на номинал промежуточной частоты.
Для определенности будем считать, что 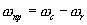 . Очевидно, что в результате перемножения входного
. Очевидно, что в результате перемножения входного 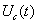 и опорного
и опорного 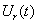 каждая из гармоник
каждая из гармоник 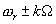 даст сумму гармонических сигналов на частотах
даст сумму гармонических сигналов на частотах 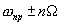 . Так как полоса резонансного фильтра принята меньше, чем интервал между гармониками (
. Так как полоса резонансного фильтра принята меньше, чем интервал между гармониками (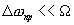 ), то из богатого спектра комбинационных частот после умножителя узкополосным фильтром будут отфильтрованы только гармонические сигналы с частотами равными промежуточной, т.е.
), то из богатого спектра комбинационных частот после умножителя узкополосным фильтром будут отфильтрованы только гармонические сигналы с частотами равными промежуточной, т.е.
Результирующий гармонический сигнал промежуточной частоты на выходе резонансного фильтра есть векторная сумма „парциальных“ сигналов, получаемых от взаимодействия каждой гармоники спектра 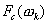 с соответствующей гармоникой спектра опорного гетеродина
с соответствующей гармоникой спектра опорного гетеродина 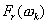 .
.
Фазы этих „парциальных“ векторов будут различны и изменяться при изменении относительного положения импульсов сигнала и гетеродина во времени. Здесь нужно различать способы формирования опорного (гетеродинного) радиоимпульса.
Первый способ — ударное возбуждение радиоимпульса: фаза ВЧ заполнения жестко привязана к огибающей. При изменении задержки 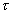 такой импульс смещается как целое. Фазы гармоник его спектра изменяются так
такой импульс смещается как целое. Фазы гармоник его спектра изменяются так 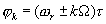 , т. е. все вектора, представляющие парциальные сигналы, вращаются, но разной „скоростью“.
, т. е. все вектора, представляющие парциальные сигналы, вращаются, но разной „скоростью“.
Векторная сумма зависит от взаимного положения „парциальных“ векторов, от их взаимных разностей фаз Качественно картина меняется так: при разносе импульсов во времени эти вектора расположены „веером“ так, что их векторная сумма равна нулю. При частичном перекрытии „веер“ частично „схлопывается“, что дает некоторую отличную от нуля амплитуду суммарного сигнала. Наконец, при совпадении импульсов во времени „веер“ складывается, все „парциальные“ вектора оказываются в фазе, что обеспечивает максимальное значение результирующей амплитуды сигнала промежуточной частоты.
Заметим, что фаза результирующего сигнала промежуточной частоты (положение суммарного вектора) будет изменяться на всем интервале изменения задержки 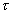 , от начала „перекрытия“ импульсов (
, от начала „перекрытия“ импульсов ( ) во времени, до полного их разноса (
) во времени, до полного их разноса (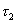 ).
).
Сказанное качественно иллюстрируется рис. 21,22.
Рис.21
Рис.22
Рассмотрим другой способ формирования опорных радиоимпульсов, импульсов гетеродина. При этом способе из непрерывного гармонического сигнала на частоте 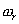 путем импульсной амплитудной модуляции формируется также периодическая последовательность опорных радиоимпульсов. Очевидно, что в этом варианте фаза и огибающая опорных импульсов не будут жестко связаны. Покажем, что при этом фаза сигнала промежуточной частицы на выходе узкополосного резонансного фильтра не будет зависеть от взаимного временного положения периодических последовательностей входного и опорного сигналов. Дело в том, что при формировании опорных импульсов путем модуляции при изменении задержки модулирующего видеоимпульса фаза гармоники на центральной частоте спектра
путем импульсной амплитудной модуляции формируется также периодическая последовательность опорных радиоимпульсов. Очевидно, что в этом варианте фаза и огибающая опорных импульсов не будут жестко связаны. Покажем, что при этом фаза сигнала промежуточной частицы на выходе узкополосного резонансного фильтра не будет зависеть от взаимного временного положения периодических последовательностей входного и опорного сигналов. Дело в том, что при формировании опорных импульсов путем модуляции при изменении задержки модулирующего видеоимпульса фаза гармоники на центральной частоте спектра 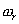 остается постоянной. Гармоники же в верхней
остается постоянной. Гармоники же в верхней 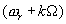 и нижней полосах
и нижней полосах 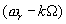 этого спектра будут получать при изменении
этого спектра будут получать при изменении 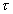 приращения фаз разных знаков
приращения фаз разных знаков 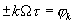 . Это приводит к тому, что после перемножения со входным сигналом и фильтрации узкополосным резонансным фильтром „парциальных“ сигналов на частоте
. Это приводит к тому, что после перемножения со входным сигналом и фильтрации узкополосным резонансным фильтром „парциальных“ сигналов на частоте 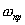 результирующий сигнал на этой частоте не будет изменять своей фазы при изменении задержки. Это утверждение справедливо при условии, что спектры как принимаемого
результирующий сигнал на этой частоте не будет изменять своей фазы при изменении задержки. Это утверждение справедливо при условии, что спектры как принимаемого 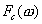 , так и опорного (гетеродинного) сигналов симметричны относительно своих несущих частиц ВЧ заполнения. Качественно зависимость параметров выходного сигнала от задержки
, так и опорного (гетеродинного) сигналов симметричны относительно своих несущих частиц ВЧ заполнения. Качественно зависимость параметров выходного сигнала от задержки 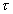 так же удобно проиллюстрировать с помощью векторных диаграмм, аналогичных рассмотренным выше.
так же удобно проиллюстрировать с помощью векторных диаграмм, аналогичных рассмотренным выше.
Различие будет лишь в том, что направление (аргумент) вектора парциального сигнала от взаимодействия центральных частот спектров входного и опорного сигналов остается постоянным при изменении задержки на интервале 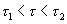 . Тогда как „парциальные“ вектора , соответствующие верхней и нижней полосам спектров при изменении
. Тогда как „парциальные“ вектора , соответствующие верхней и нижней полосам спектров при изменении 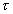 теперь вращаются в разные стороны, образуя опять „веера“. Понятно, что векторная сумма будет зависеть от степени раскрытия такого»веера «, причем аргумент суммарного вектора будет сохранять свою величину, так как „парциальные“ вектора , соответствующие верхней и нижней полосе спектра, получают симметричные приращения, но разных знаков, „Веер“ остается симметричным с неподвижным центральным вектором. Модуль суммарного вектора будет описываться взаимокорреляционной функцией
теперь вращаются в разные стороны, образуя опять „веера“. Понятно, что векторная сумма будет зависеть от степени раскрытия такого»веера «, причем аргумент суммарного вектора будет сохранять свою величину, так как „парциальные“ вектора , соответствующие верхней и нижней полосе спектра, получают симметричные приращения, но разных знаков, „Веер“ остается симметричным с неподвижным центральным вектором. Модуль суммарного вектора будет описываться взаимокорреляционной функцией 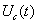 и
и 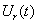 , зависящей от
, зависящей от 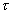 .
.
Рис.23
Рассмотрим теперь возможный вариант, когда значения частот заполнения радиоимпульсов принимаемого и опорного совпадают. В этом случае после перемножителя следует включить узкополосный низкочастотный фильтр, выделяющий „постоянную“ составляющую, величина и знак которой будут изменяться при изменении относительного положения принимаемого и опорного импульсов во времени. Такой выходной сигнал будет описываться взаимокорреляционной функцией. Вид этой функции (при равной длительности импульсов) качественно изображен на рис 23. ,а описывается она формулой (4.34). Выходной сигнал в этом случае описывается осциллирующей функцией по аргументу t — относительному сдвигу этих импульсов во времени. Понятно, что для периодически повторяющихся импульсов их взаимокорреляционная функция будет также периодической по t с периодом их следования.
Рис. 24
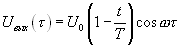
При
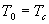
и 0
Оценим теперь отношение сигнал/шум на выходе корреляционного гребенчатого
фильтра, оптимального для приёма периодической последовательности радиоимпульсов. Выше было показано, что оптимальный фильтр для гармонического сигнала обеспечивает отношение сигнал/ шум по мощности (4.28)
Гдеb=Dw — полоса узкополосного резонансного фильтра.
В данном случае оптимальный фильтр для приёма периодической последовательности радиоимпульсов имеет также единственный резонансный фильтр с узкой полосой. Поэтому для каждого „зубца“ гребёнки и каждой гармоники спектра входного сигнала будем иметь такое же отношение сигнал/шум, как и для элементарного гармонического сигнала. По отношению к входному сигналу умножитель — это линейное параметрическое устройство. Поэтому результат воздействия спектра гармоник и результат воздействия шума можно рассматривать независимо.
Относительно гармоник спектра сигнала выше было показано, что при совмещении во времени радиоимпульсов входной и опорной последовательностей радиоимпульсов все гармоники парциальных составляющих спектра на частоте 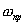 . суммируются в фазе. („веер“ парциальных векторов схлопывается). Составляющие шума, прошедшие отдельные зубцы гребёнки тоже сложатся, но по мощности! Поэтому можно считать, что эффективная полоса для шума будет определяться суммой полос отдельных полос зубцов гребёнки:
. суммируются в фазе. („веер“ парциальных векторов схлопывается). Составляющие шума, прошедшие отдельные зубцы гребёнки тоже сложатся, но по мощности! Поэтому можно считать, что эффективная полоса для шума будет определяться суммой полос отдельных полос зубцов гребёнки: 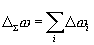 (4.30).
(4.30).
Число членов в этой сумме ограничено и определяется эффективной шириной спектра опорных радиоимпульсов (импульсов гетеродина). Кроме того, ширина спектра мощности шума ограничивается входным полосовым фильтром. Поэтому искомое отношение сигнал/шум на выходе оптимального корреляционного фильтра определится так:
По мощности:
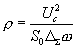
, а по амплитуде
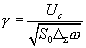
(4.31)
В заключение обратим внимание, что в рассмотренном варианте гребёнчатая АЧХ реализуется за счёт линейчатого спектра (с некоторой эффективной шириной) импульсного опорного сигнала и единственного узкополосного резонансного усилителя промежуточной частоты. При этом, ширина полосы этого усилителя должна быть много меньше, чем интервал между частотами гармоник опорного сигнала (гетеродина).
Такой аналоговый коррелятор был реализован и практически использовался в станции наклонного зондирования ионосферы средневолнового диапазона. Для возможности оценки не только амплитуды и групповой задержки, но и фазы высокочастотного заполнения отраженных от ионосферы радиоимпульсов после узкополосного усилителя сигнал промежуточной частоты подавался на два параллельных фазовых детектора. Опорные гармонические сигналы на фазовых детекторах имели номинал 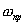 и были сдвинуты по фазе на
и были сдвинуты по фазе на 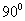 . Таким образом, на выходах фазовых детекторов получались синусная и косинусная составляющие огибающих суммарного сигнала. Это позволяло оценить соответствующие фазовые сдвиги высокочастотного заполнения „земного“ и отраженного радиоимпульсов, при условии, что эти радиоимпульсы были разделены во времени.
. Таким образом, на выходах фазовых детекторов получались синусная и косинусная составляющие огибающих суммарного сигнала. Это позволяло оценить соответствующие фазовые сдвиги высокочастотного заполнения „земного“ и отраженного радиоимпульсов, при условии, что эти радиоимпульсы были разделены во времени.
Пример наблюдаемой картинки на экране индикатора станции приведен на рис. Далее этот сигнал оцифровывался с помощью АЦП и поступал в ЭВМ для обработки.
При используемых параметрах зондирующих радиоимпульсов в диапазоне средних волн „земной“ и отраженный от ионосферы сигналы уверенно разделялись во времени. Величина задержки отраженного сигнала в приводимом эксперименте порядка 220 мкс.
Частота ВЧ заполнения радиоимпульсов приблизительно 350 кГц, приём велся на удалении 220 км. Приёмная аппаратура аналогово коррелятора имела узкополосный усилитель с шириной полосы 5 Гц, при частоте повторения излучаемых импульсов 625 Гц. Это позволяло надёжно выделить полезные сигналы на фоне шумов и помех в весьма загруженном СВ диапазоне, обеспечивался выигрыш в отношении сигнал/шум более30-тина выходе приёмного аналогово коррелятора по отношению ко входу. Очевидно, что располагая сигналом в цифровой форме было возможно и дальнейшее повышение отношения сигнал/шум, используя накопление.
4.5.3. Оценка возможного выигрыша в отношении сигнал / шум при дискретной записи сигнала.
Выше было показано, что для периодического сигнала отношение сигнал / шум может быть улучшено накоплением. Возможный выигрыш пропорционален квадратному корню из времени накопления и обратно пропорционален полосе аналогово фильтра. В случае дискретных отсчётов сигнала — аддитивной смеси сигнал + шум, очевидно, что выигрыш будет пропорционален 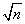 , где n число равноотстоящих отсчётов. Процесс накопления удобно реализовать с помощью алгоритма — программы на ЭВМ. При практической реализации этого способа следует иметь в виду, что число накапливаемых выборок, дающих желаемый выигрыш будет ограничено разрядностью применяемого аналого-цифрового преобразователя (АЦП). Можно задаться вопросом о необходимой разрядности АЦП, если задан требуемый выигрыш С / Ш. Или оценить возможный выигрыш, если АЦП уже выбран. Тот факт , что АЦП присущи собственные шумы в данном пособии рассматриваться не будет. Эти вопросы освещены в специальной литературе. Будут учтены только» шумы дискретизации «.
, где n число равноотстоящих отсчётов. Процесс накопления удобно реализовать с помощью алгоритма — программы на ЭВМ. При практической реализации этого способа следует иметь в виду, что число накапливаемых выборок, дающих желаемый выигрыш будет ограничено разрядностью применяемого аналого-цифрового преобразователя (АЦП). Можно задаться вопросом о необходимой разрядности АЦП, если задан требуемый выигрыш С / Ш. Или оценить возможный выигрыш, если АЦП уже выбран. Тот факт , что АЦП присущи собственные шумы в данном пособии рассматриваться не будет. Эти вопросы освещены в специальной литературе. Будут учтены только» шумы дискретизации «.
В этом приближении рассмотрим связь возможного выигрыша С/ Ш при накоплении на АЦП с заданной разрядностью.
Пусть мгновенное значение входной величины есть :
V = U +
z и отношение С / Ш
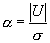
,
Где U -величина сигнала,  - среднеквадратичная величина шума.
- среднеквадратичная величина шума.
Интересуемся случаем, когда a соответствует максимальному значению числа., минимальный код 1 (число > 0). Считаем, что шумы распределены по нормальному закону.. Ограничим диапазон АЦП утроенной среднеквадратичной величиной шума (3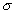 ), что будет соответствовать максимальному коду. Уровень 3
), что будет соответствовать максимальному коду. Уровень 3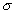 при нормальном законе распределения ограничит значения шума только в 0.1% случаев. Считая, что динамический диапазон преобразователя установлен 3s, можно ввести коэффициент передачи код -напряжение :
при нормальном законе распределения ограничит значения шума только в 0.1% случаев. Считая, что динамический диапазон преобразователя установлен 3s, можно ввести коэффициент передачи код -напряжение :
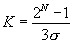
(4.32)
Дискретная форма представления числа приводит к»шумам оцифровки «.

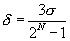
(4.33).
Это шум оцифровки, оцениваемый единицей кода , пересчитанной ко входу.
Отношение сигнал / цифровые шумы есть
Цифровые шумы не снимаются накоплением, поэтому величина b определяет предельно достижимое отношение С / Ш на выходе при данной разрядности , а отношение b/a возможный выигрыш при цифровом
накоплении Оценим теперь возможный выигрыш при данной разрядности. Исходим из того, что при накоплении отношение С / Ш улучшается пропорционально 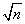 . Приравнивая эти величины , имеем :
. Приравнивая эти величины , имеем :
Или
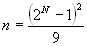
,
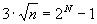
(4.35 ).
Наконец , задаваясь желаемым выигрышем при цифровом накоплении , определяем требуемую разрядность АЦП и ЭВМ .
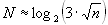
при
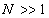
(4.36).
Полученные приближенные формулы могут оказаться полезными при выборе типа АЦП или при оценке достижимого выигрыша при цифровом накоплении с данным АЦП.
Можно уточнить приведённую оценку» шума оцифровки«- d, если учесть, что как только значение входного сигнала V = U+x окажется вблизи середины шага оцифровки то ,из-за случайного характера шума в АЦП , может быть добавлена или вычтена единица кода. Для приближенной оценки можно на интервале шага оцифровки распределение шума считать равномерным. Тогда дисперсия оцифровки оцениваеtтся так :
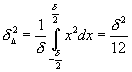

(4.37).
Таким образом реальная величина «шума оцифровки» оказывается меньше.
Оптимальное выделение сигнала из шума можно проводить различными методами, в зависимости от того, какая ставится задача — обнаружение сигнала, сохранение формы сигнала и т.д. В каждом методе оптимальной фильтрации вводится понятие критерия оптимальности, согласно которому строится оптимальный алгоритм обработки сигнала [ 11].
Конкретный алгоритм оптимальной фильтрации будет существенно зависеть от того непериодический или периодический сигнал должен быть выделен (обнаружен) на фоне шума. По отношению к периодическому сигналу далее различаются ситуации: известна или нет его частота повторения. Ниже эти варианты задач будут рассмотрены последовательно.
3.1 Оптимальная фильтрация непериодического (одиночного) сигнала
Оценим возможную эффективность обнаружения непериодического сигнала при его аддитивной смеси с белым шумом. При формулировке задачи нахождения коэффициента передачи «оптимального» фильтра используются существенные требования относительно сигнала: во-первыхсчитается известной форма сигнала f(t) и соответственно его спектр  , во вторых сигнал считается ограниченным во времени:
, во вторых сигнал считается ограниченным во времени:

(3.1)
Т.е. сигнал имеет конечную длительность.
Определение оптимальности фильтра формулируется следующим образом:
Оптимальным фильтром в задаче обнаружения одиночного импульса конечной длительности является фильтр, обеспечивающий максимальное отношение пиковой мощности сигнала к мощности шума в момент окончания импульса.
Комплексный коэффициент передачи такого оптимального фильтра прямо определяется спектром заданного, подлежащего обнаружению сигнала (т.е. его формой и длительностью  ) [2 ]
) [2 ]
Так, если сигнал имеет спектр

(3.2)
и длительность его  , то функция
, то функция
есть функция комплексно сопряженная функции спектральной плотности сигнала.
Можно показать [2], что комплексный коэффициент передачи оптимального фильтра, в приведенном выше смысле определяется так:
или
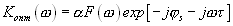
(3.3)
Не воспроизводя выкладки доказательства формулы (3.3) приведенных в ряде источников (например [ 2] ), остановимся на физическом смысле результата.
Замечая, что фазовая характеристика коэффициента передачи в (3.3) есть
видим, что  — компенсирует фазовые сдвиги составляющих сдвиги спектра сигнала (3.2), что формирует «пик» импульса на выходе, а линейная функция —
— компенсирует фазовые сдвиги составляющих сдвиги спектра сигнала (3.2), что формирует «пик» импульса на выходе, а линейная функция —  обеспечивает задержку этого «пика» на время длительности сигнала, т. е. этот пик приходится на момент окончания сигнала.. Можно сказать, что обеспечивается накопление полезного сигнала на интервале всего времени существования импульса.
обеспечивает задержку этого «пика» на время длительности сигнала, т. е. этот пик приходится на момент окончания сигнала.. Можно сказать, что обеспечивается накопление полезного сигнала на интервале всего времени существования импульса.
Формула (3.3) устанавливает также, что модуль коэффициента передачи должен совпадать с модулем спектральной плотности функции заданного сигнала, т. е. оптимальный фильтр ослабляет спектральные составляющие шума тем сильнее, чем меньше модуль  , В результате полная мощность шума на выходе фильтра оказывается меньшей, чем при равномерной АЧХ.
, В результате полная мощность шума на выходе фильтра оказывается меньшей, чем при равномерной АЧХ.
Наконец отметим, что произвольная константа  размерна. При безразмерном
размерна. При безразмерном 
 имеет размерность обратной спектральной плотности сигнала.
имеет размерность обратной спектральной плотности сигнала.
3.2. Оценка отношения сигнал/шум при оптимальном фильтре
Будем исходить из приведенного выше выражения (3.3). Заметим, что для сигнала (импульса) сложной формы синтез оптимального фильтра является не простой задачей. По этому искомую оценку отношения сигнал/шум проведем на примере прямоугольного импульса.
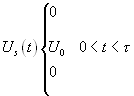
(3.4)
Рис.1
Будем считать, что полезный сигнал представляет собой одиночный прямоугольный импульс (3.4) длительностью  и с напряжением
и с напряжением  , изображенный на рис 1.
, изображенный на рис 1.
Его спектральная плотность описывается функцией

и сопряженная

следовательно, для данного импульса в соответствии с (3.3) имеем:

(3.5).
Такой коэффициент передачи может быть обеспечен схемой рис 2.
Рис.2
Содержащей идеальное интегрирующее звено ( ), линию задержки (
), линию задержки ( ) и схему вычитания .
) и схему вычитания .
Найдем сигнал на выходе оптимального фильтра для рассматриваемого примера ( =1)
=1)
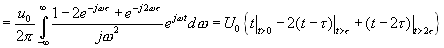
(3.6).
Таким образом, импульс на выходе имеет треугольную форму с основанием 2t и максимальным значением U0 при t=t . Оценим теперь мощность шума на выходе этого оптимального фильтра. Используем формулы (3.3) и (3.5). Положим a =1 Будем считать шум ’ белым’.
Рис.3
Представим модуль оптимального коэффициента передачи в виде

(3.7)
Мощность шума на выходе фильтра в соответствии с (2.2 ) и (2.3) определиться так

(3.8).
Этот табличный интеграл [3] имеет значение:  . Таким образом, искомая величина мощности шума равна:
. Таким образом, искомая величина мощности шума равна:
откуда искомое отношение мощности сигнала к мощности шума для данного оптимального фильтра будет:

(3.10).
а для отношения амплитуд сигнал/шум

(3.11).
В заключение еще раз отметим, что оптимальный фильтр, построенный по указанному выше критерию, жестко связан с полезным входным сигналом: изменение полезного входного сигнала ведет к необходимости изменения коэффициента передачи фильтра.
3.3. Определение оптимальной полосы фильтра нижних частот в задаче выделения (обнаружения) одиночного сигнала на фоне белого шума
Учитывая сложность задачи синтеза оптимального фильтра , в результате которого находится его функция  можно подойти к задаче по другому.
можно подойти к задаче по другому.
Сигналу выбирается тип АЧХ фильтра, сообразуясь с формой сигнала-импульса (точнее модулем его спектра). Например, для рассмотренного выше прямоугольного импульса выбирается фильтр НЧ, для импульса с высокочастотным заполнением- резонансный фильтр и т.д. Далее задача оптимизации ставится относительно выбора параметра фильтра — полосы его пропускания. Следуя этому подходу далее рассматривается возможность выделения полезного сигнала из белого шума не с помощью описанного выше оптимального фильтра, а с помощью линейного RC фильтра нижних частот. При этом полоса фильтра будет выбираться таким образом, чтобы достигнуть максимально возможного (для фильтра нижних частот) энергетического соотношения сигнал/шум к концу импульса.
Пусть полный входной сигнал U(t) выражается в виде суммы полезного входного сигнала  и белого шума
и белого шума  — случайного процесса, у которого спектральная плотность
— случайного процесса, у которого спектральная плотность  не зависит от частоты
не зависит от частоты
 (3.12).
(3.12).
В качестве фильтра нижних частот будем рассматривать интегрирующую цепочку (рис 4) — низкочастотный фильтр первого порядка с постоянной времени  и коэффициентом передачи
и коэффициентом передачи

(3.13).
Рис. 4
При исследовании прохождения шума через линейную систему будем использовать формулу (2.3) ,квадрат модуля коэффициента передачи

(3.14).
где  — полоса пропускания рассматриваемого фильтра нижних частот по уровню 0.707. Требуется найти полосу
— полоса пропускания рассматриваемого фильтра нижних частот по уровню 0.707. Требуется найти полосу  заданного фильтра нижних частот, обеспечивающую максимальное отношение сигнал/шум на выходе фильтра.
заданного фильтра нижних частот, обеспечивающую максимальное отношение сигнал/шум на выходе фильтра.
Можно рассматривать прохождение через фильтр нижних частот полезного сигнала и шума раздельно, так как интегрирующая цепочка — линейная схема.
3.3.1. Прохождение полезного сигнала через однозвенный RC фильтр нижних частот
Сигнал на выходе линейной системы может быть найден с помощью спектрального метода.

(3.15).
где коэффициент передачи интегрирующей цепочки определяется формулой (3.14) , а спектральная плотность полезного входного сигнала (3.4) была найдена как интеграл Фурье

(3.16).
Подставив в (3.15) формулы (3.16) и (3.13) и вычислив интеграл, получаем следующее выражение для сигнала на выходе фильтра

при

(3.17)


Рис 5.
Таким образом, выходной сигнал достигает своего максимального значения в момент окончания входного импульса t=t

(3.18).
Это выражение зависит от соотношения полосы частот фильтра 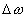 (3.13) и полосы частот, занимаемой полезным сигналом
(3.13) и полосы частот, занимаемой полезным сигналом  , которая связана с длительностью прямоугольного импульса так
, которая связана с длительностью прямоугольного импульса так 
 1/t . С учетом этого выражение (3.18) можно преобразовать следующим образом
1/t . С учетом этого выражение (3.18) можно преобразовать следующим образом

(3.19).
Если полоса частот, занимаемая спектральной плотностью полезного входного сигнала, меньше полосы частот, определяемой коэффициентом передачи интегрирующей цепочки 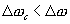 , то максимальное значение полезного сигнала на выходе интегрирующей цепочки (3.18) равно
, то максимальное значение полезного сигнала на выходе интегрирующей цепочки (3.18) равно  и не зависит от полосы фильтра
и не зависит от полосы фильтра 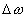 при
при 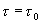 .
.
Если же полоса частот, занимаемая спектральной плотностью полезного входного сигнала, больше полосы частот, занимаемой коэффициентом передачи интегрирующей цепочки,  , то разложив экспоненту в выражении (3.18) в ряд, получаем следующее максимальное значение полезного сигнала на выходе интегрирующей цепочки
, то разложив экспоненту в выражении (3.18) в ряд, получаем следующее максимальное значение полезного сигнала на выходе интегрирующей цепочки
В этом случае амплитуда полезного сигнала на выходе фильтра линейно зависит от полосы фильтра  .
.
Мощность полезного входного сигнала, входящая в энергетическое отношение сигнал/шум, будет пропорциональна, таким образом, квадрату от полосы фильтра
Следовательно, если полоса фильтра перекрывает полосу полезного входного сигнала, то дальнейшее увеличение полосы фильтра не приводит к увеличению полезного выходного сигнала. Если же полоса фильтра уже полосы сигнала, то увеличение полосы фильтра приводит к увеличению мощности полезного выходного сигнала, пропорционально квадрату полосы фильтра.
3.3.2. Прохождение случайного сигнала (белого шума) через фильтр нижних частот
Для мощности шума на выходе фильтра с помощью формул (2.2) и (2.3) может быть получено следующее выражение
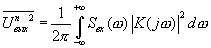
(3.20),
в котором положим  — спектральная плотность мощности белого шума, а квадрат модуля коэффициента передачи определен формулой (3.14). Вычислив интеграл , получаем
— спектральная плотность мощности белого шума, а квадрат модуля коэффициента передачи определен формулой (3.14). Вычислив интеграл , получаем

(3.21),
где  — ширина полосы фильтра по уровню 1/
— ширина полосы фильтра по уровню 1/ .
.
Отсюда следует, что мощность шума на выходе фильтра линейно зависит от полосы коэффициента передачи интегрирующей цепочки.
Используя полученные выражения для максимального значения выходного полезного сигнала (3.18) и мощности шума на выходе фильтра (3.21), можно получить выражение для энергетического отношения сигнал/шум на выходе фильтра нижних частот (RC-цепочки):

(3.22),
где

и

(3.23)
Искомую величину оптимальной полосы  для выбранного НЧ фильтра (3.13) и сигнала (3.4), обеспечивающей максимальное отношение сигнал/шум в момент t=t , найдем из условия максимума функции (3.23), т.е .
для выбранного НЧ фильтра (3.13) и сигнала (3.4), обеспечивающей максимальное отношение сигнал/шум в момент t=t , найдем из условия максимума функции (3.23), т.е .

(3.24).
Функция  имеет пологий максимум, ее график приведен на рис 6.
имеет пологий максимум, ее график приведен на рис 6. 
Рис. 6
Таким образом
И следовательно отношение пиковой мощности сигнала и мощности шума при оптимальной полосе НЧ фильтра равно

(3.25).
Отношение же амплитуды сигнала к «амплитуде» шума будет

(3.26).
Напомним, что использование фильтра с оптимальным коэффициентом передачи(3.5) приводило к отношению сигнал/шум по мощности равному (3.10)

(3.10).
Сравнивая (3.10) с (3.25), видим, что использование RC фильтра НЧ (3.13) с правильно выбранной полосой вместо фильтра с оптимальным коэффициентом передачи приводит к ухудшению соотношения сигнал/шум по мощности на 19 %.

(3.27),
и лишь на 10% по отношению амплитуд сигнал/шум
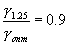
(3.28).
Т.о. для конкретного сигнала — прямоугольного импульса использование простого RC фильтра НЧ можно считать оправданным (целесообразным).
Качественно такой результат понятен. Если полоса фильтра уже полосы сигнала, то целесообразно увеличивать полосу фильтра, так как при этом мощность полезного сигнала на выходе растет пропорционально квадрату полосы, а мощность шума растет пропорционально первой степени полосы. Если полоса фильтра шире полосы сигнала, то целесообразно уменьшать полосу фильтра, так как при этом мощность полезного сигнала на выходе не меняется, а мощность шума уменьшается пропорционально первой степени полосы.
Далее найдем соотношение сигнал/шум для многозвенного RC — фильтра низкой частоты.
3.4 Определение оптимальной полосы многозвенного фильтра нижних частот
Рассмотрим теперь задачу определения оптимальной полосы многозвенного фильтра с целью обеспечения максимального отношения сигнал/шум в момент окончания импульса. Импульс будем, как и раньше, считать прямоугольным.(3.4). Конкретно рассмотрим фильтр, собранный идентичных RC — звеньев, разделенных буферными каскадами.(рис 7).
Рис 7.
Коэффициент передачи такого фильтра описывается функцией
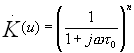
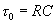
(3.29)
Если зафиксировать полосу пропускания этого фильтра  на заданном уровне неравномерности
на заданном уровне неравномерности  , то эти два параметра, как это следует из (3.29), оказываются связанными уравнением
, то эти два параметра, как это следует из (3.29), оказываются связанными уравнением

(3.30).
Отсюда очевидно, что для обеспечения постоянства общей заданной полосы фильтра  при изменении числа звеньев n, постоянную
при изменении числа звеньев n, постоянную 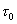 необходимо изменить следующим образом
необходимо изменить следующим образом

(3.31).
При увеличении числа звеньев n, будет увеличиваться крутизна спада АЧХ в области частот, выше заданной полосы  . (рис 8).
. (рис 8).
Рис8.
Переходная характеристика h(t) для рассматриваемого фильтра (3.29) — реакция на включение ступеньки напряжения на входе определяется так:

(3.32).
где  , как отмечено выше, если при увеличении числа каскадов n ставится требование
, как отмечено выше, если при увеличении числа каскадов n ставится требование  =const ( на заданном уровне неравномерности
=const ( на заданном уровне неравномерности  ), то параметр
), то параметр  каждого каскада должен изменятся в соответствии с формулой (3.31). Пример зависимости
каждого каскада должен изменятся в соответствии с формулой (3.31). Пример зависимости 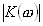 от n для n=1 и n=5 при одинаковой
от n для n=1 и n=5 при одинаковой  приведен на рис.8, а зависимость переходной характеристики h(t) также при n=1 и n=5 приведен на рис.9.
приведен на рис.8, а зависимость переходной характеристики h(t) также при n=1 и n=5 приведен на рис.9.
Оценим теперь уровень шума на выходе фильтра. Считаем шум на выходе белым, имеющим спектральную плотность мощности S0

(3.33).
Значение этого табличного неопределенного интеграла (3.36) известно [ 3].

(3.34).
При вычислении определенного интеграла (3.34) следует учесть, что функция  равна нулю на верхнем (
равна нулю на верхнем (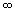 ) и на нижнем (-
) и на нижнем (-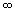 ) пределах. Поэтому
) пределах. Поэтому
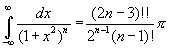
(3.35).
Учитывая также необходимое изменение RC каждого каскада фильтра при увеличении n (при требовании  =const) получаем интересующий количественный результат. В качестве примера приводим численные данные расчета мощности шума и напряжения шума для фильтров разных порядков (n).
=const) получаем интересующий количественный результат. В качестве примера приводим численные данные расчета мощности шума и напряжения шума для фильтров разных порядков (n).
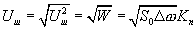
и
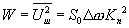
(3.36).
|
n
|
1
|
2
|
3
|
4
|
5
|
6
|
|

|
0.707
|
0.78
|
0.85
|
0.9
|
0.95
|
1.01
|
|

|
0.5
|
0.61
|
0.72
|
0.81
|
0.91
|
1.025
|
Полученные выше данные о прохождении импульсного сигнала и белого шума через n-звенныйфильтр низкой частоты позволит определить оптимальную полосу фильтра ( при заданной длительности импульса) и соотношение сигнал/шум на выходе рассматриваемого фильтра в момент окончания импульс t=t при оптимальном выборе его полосы  . Как и в случае однозвенного фильтра строим функцию отношения величины полученного сигнала к «амплитуде» шума
. Как и в случае однозвенного фильтра строим функцию отношения величины полученного сигнала к «амплитуде» шума

(3.37).
Здесь  ,
,  -коэффициент изменения RC=
-коэффициент изменения RC=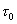 каждого звена, при изменении порядка фильтра n (3.31)
каждого звена, при изменении порядка фильтра n (3.31)
Отношение  , как функция
, как функция  ,имеет пологий max, зависящий от порядка фильтра n.
,имеет пологий max, зависящий от порядка фильтра n.
Так, например, для трехзвенного фильтра max  достигается при
достигается при  , и значении
, и значении  . Для пятизвенного фильтра получаем
. Для пятизвенного фильтра получаем  и
и  . Из этих значений определяется оптимальная величина параметра фильтра
. Из этих значений определяется оптимальная величина параметра фильтра  .
.
Т.о. искомое отношение амплитуд сигнал/шум с учетом коэффициентов Ki в соответствии с выражением (3.37) дает:
Для трехзвенного фильтра

(3.38),
Для пятизвенного фильтра

(3.39).
Сравнивая эти результаты с полученными ранее, видим, что повышение порядка фильтра дает худшее отношение сигнал/шум, чем для фильтра первого порядка (3.13):

и

(3.40).
Поэтому, если «оптимальный» фильтр определяемый требованием  (см(3.3)) заменяется фильтром RC с оптимально подбираемым параметром, то в рассматриваемом случае прямоугольного импульса лучшим оказывается простейший RC фильтр первого порядка .
(см(3.3)) заменяется фильтром RC с оптимально подбираемым параметром, то в рассматриваемом случае прямоугольного импульса лучшим оказывается простейший RC фильтр первого порядка .
Этому предпочтению можно дать следующие объяснения.
Во-первых, АЧХ RC фильтр первого порядка оказывается ближе к модулю спектра прямоугольного импульса, чем АЧХ фильтров более высоких порядков. Напомним, что для «оптимального» фильтра в соответствии с (3.3) оказывается, что его АЧХ совпадает с модулем спектра сигнала.
Во-вторых, как показано выше, значение обобщенного параметра  , обеспечивающего наибольшее отношение мощности сигнала к мощности шума в конце импульса, увеличивается с повышением порядка фильтра. Так например, при n=1 значение
, обеспечивающего наибольшее отношение мощности сигнала к мощности шума в конце импульса, увеличивается с повышением порядка фильтра. Так например, при n=1 значение  , при n=3 имеем, что
, при n=3 имеем, что 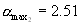 , а при n=5 обобщённый параметр
, а при n=5 обобщённый параметр 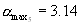 .
.
Поэтому при заданной длительности импульса t полоса фильтра 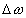 , требуется большей, для фильтра более высокого порядка, что также приводит к повышению шума.
, требуется большей, для фильтра более высокого порядка, что также приводит к повышению шума.
Физически последнюю зависимость от n можно объяснить ростом группового запаздывания, т. е. требуемое максимальное отношение
к концу импульса достигается для больших n при больших значениях  . Что при фиксированной длительности импульса означает большее значение
. Что при фиксированной длительности импульса означает большее значение  . А это , естественно, увеличивает шум на выходе фильтра.
. А это , естественно, увеличивает шум на выходе фильтра.
Введем спектральную плотность автокорреляционной функции случайного процесса S( ), связанную с автокорреляционной функцией
), связанную с автокорреляционной функцией  преобразованием Фурье
преобразованием Фурье

,

(2.1)
Спектральная плотность автокорреляционной функции случайного процесса  описывает мощность случайного процесса, приходящуюся, на заданный интервал частот, поэтому часто эту функцию называют спектральной плотностью мощности случайного процесса. Вследствие четности автокорреляционной функции (1.11) ее спектральная плотность
описывает мощность случайного процесса, приходящуюся, на заданный интервал частот, поэтому часто эту функцию называют спектральной плотностью мощности случайного процесса. Вследствие четности автокорреляционной функции (1.11) ее спектральная плотность  является вещественной функцией.
является вещественной функцией.
В отличие от спектрального описания детерминированных функций, когда с помощью преобразования Фурье по заданному частотному спектру можно определить временную форму сигнала, спектральное описание случайного процесса (1.15) проводится для его статистической характеристики — автокорреляционной функции.С помощью выражения (2.1) можно выразить среднюю мощность случайного процесса через  :
:

(2.2)
а мощность флуктуационной составляющей случайного процесса- дисперсия случайного процесса — может быть найдена с помощью выражения (1.9). При оптимальной фильтрации сигналов из шумов часто пользуются понятием «белого» шума. Белым шумом называется случайный процесс, у которого спектральная плотность автокорреляционной функции не зависит от частоты  = S0 . Это соответствует тому, что мощность белого шума равномерно распределена по всему частотному диапазону. Белый шум- идеализированный случайный процесс, так как его автокорреляционная функция описывается дельта функцией Дирака, а дисперсия такого процесса бесконечна. Однако, в случае постоянства спектральной плотности мощности случайного процесса в рассматриваемом конечном диапазоне частот, введение такой идеализации позволяет разрабатывать достаточно легко применимые оптимальные методы фильтрации. Пример белого шума — тепловые шумы транзисторов в диапазоне частот от 0 до
= S0 . Это соответствует тому, что мощность белого шума равномерно распределена по всему частотному диапазону. Белый шум- идеализированный случайный процесс, так как его автокорреляционная функция описывается дельта функцией Дирака, а дисперсия такого процесса бесконечна. Однако, в случае постоянства спектральной плотности мощности случайного процесса в рассматриваемом конечном диапазоне частот, введение такой идеализации позволяет разрабатывать достаточно легко применимые оптимальные методы фильтрации. Пример белого шума — тепловые шумы транзисторов в диапазоне частот от 0 до  , где к- постоянная Больцмана, T- абсолютная температура, а h — постоянная Планка. Понятие «белый шум» определяет только спектральную характеристику случайного процесса и оставляет открытым вопрос о законах распределения. Белыми шумами могут быть названы случайные процессы, имеющие равномерный энергетический спектр и различные законы распределения. Спектральное описание случайного процесса оказывается черезвычайно удобным при учете влияния на них амплитудно-частотных характеристик различных устройств. Так при прохождении случайного процесса через линейную систему, можно показать, что спектральные плотности мощности случайного процесса на входе
, где к- постоянная Больцмана, T- абсолютная температура, а h — постоянная Планка. Понятие «белый шум» определяет только спектральную характеристику случайного процесса и оставляет открытым вопрос о законах распределения. Белыми шумами могут быть названы случайные процессы, имеющие равномерный энергетический спектр и различные законы распределения. Спектральное описание случайного процесса оказывается черезвычайно удобным при учете влияния на них амплитудно-частотных характеристик различных устройств. Так при прохождении случайного процесса через линейную систему, можно показать, что спектральные плотности мощности случайного процесса на входе 
 и на входе
и на входе 
 линейной системы связаны следующим соотношением [ 2 ]
линейной системы связаны следующим соотношением [ 2 ]

(2.3)
Где  -комплексный коэффициент передачи линейной системы.
-комплексный коэффициент передачи линейной системы.
Случайный процесс описывается статистическими характеристиками, называемыми моментами. Кроме того, важнейшими характеристиками случайного процесса являются его стационарность и эргодичность, а также спектр мощности.
1.1.Определение моментов
Одномерная плотность распределения вероятности W(x,t) определяет вероятность
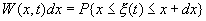
(1.1)
того, что случайная величина x (t) лежит в интервале 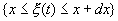 с помощью функции W(x,t) можно провести усреднение как случайной величины x (t), так и любой функции от нее.
с помощью функции W(x,t) можно провести усреднение как случайной величины x (t), так и любой функции от нее.
Средним значением случайного процесса или его первым моментом называется интеграл
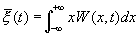
(1.2)
Второй начальный момент случайного процесса описывается интегралом
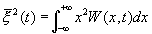
(1.3)
и определяет среднюю мощность случайного процесса.
При анализе случайных процессов часто интерес представляет флуктуационная составляющая. Введем понятие центрированного случайного процесса 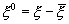
Второй центральный момент определяет мощность флуктуационной составляющей случайного процесса и называется дисперсией
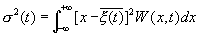
(1.4)
Аналогично можно определить также моменты случайного процесса более высокого порядка.
Таким образом, используя одномерную плотность распределения вероятности 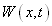 можно получить параметры случайного процесса, которые являются усреднением по множеству (ансамблю) реализаций данного случайного процесса в каком либо его «сечении», то есть в фиксированный момент времени t. Но задание одномерной плотности распределения вероятности не дает возможность определить характер изменения случайного процесса во времени и не характеризует взаимосвязь случайного процесса в различные моменты времени. Для этого вводят понятие двумерной плотности распределения вероятности
можно получить параметры случайного процесса, которые являются усреднением по множеству (ансамблю) реализаций данного случайного процесса в каком либо его «сечении», то есть в фиксированный момент времени t. Но задание одномерной плотности распределения вероятности не дает возможность определить характер изменения случайного процесса во времени и не характеризует взаимосвязь случайного процесса в различные моменты времени. Для этого вводят понятие двумерной плотности распределения вероятности 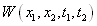 , описывающей связь двух значений
, описывающей связь двух значений 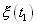 и
и  в произвольные моменты времени
в произвольные моменты времени  1 и
1 и 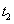 .
.

( 1.5)
С помощью двумерной плотности распределения вероятности можно определить автокорреляционную (ковариационную) функцию

(1.6)
а также автокорреляционную функцию центрированного случайного процесса
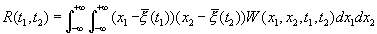
(1.7)
или
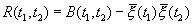
(1.8)
1.2. Стационарность случайного процесса
Случайный процесс называется стационарным, если одномерная плотность распределения вероятности и, следовательно, среднее значение и дисперсия случайного процесса не зависят от времени, а двумерная плотность распределения вероятности и автокорреляционная функция зависят только от разности временных аргументов 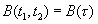 , где
, где 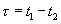 .
.
Если многомерный закон распределения вероятностей распределения мгновенных значений, взятых в разные моменты времени, не зависят от принятого начала отсчёта, а зависят только от интервалов между выбранными моментами
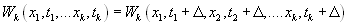
,
то такой процесс стационарен в узком смысле. Если независимость от начала отсчёта выполняется только до второго (корреляционного) момента (включая первый), то такой процесс называют стационарным в широком смысле.
1.3. Эргодичность случайного процесса
Случайный процесс называется эргодическим первого порядка, если его первый момент, полученный усреднением по множеству реализаций (1.2), с вероятностью сколь угодно близкой к единице совпадает со средним значением, полученным усреднением по времени одной достаточно длинной реализации.
Случайный процесс называется эргодическим второго порядка, если его корреляционная функция (1.6), с вероятностью сколь угодно близкой к единице совпадает со средним значением произведения случайного процесса при сдвинутых аргументах, полученным усреднением по времени одной достаточно длинной реализации.
Параметры эргодического случайного процесса могут быть определены так:
Усреднением по времени могут быть найдены также автокорреляционные функции эргодического случайного процесса
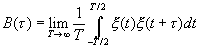
,

(1.10).
В данной работе предполагается, что аддитивно добавленный к полезному сигналу «шум» является эргодическим, случайным процессом.
1.4. Свойства корреляционных функций
Корреляционные функции — важнейшие характеристики случайных процессов.
Приведем их основные свойства:
1. 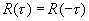 (1.11)
(1.11)
2. 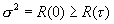 (1.12)
(1.12)
3. 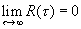
Формально можно вычислить автокорреляционную функцию (1.10) и для детерминированного процесса, например, для периодической функции
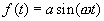
автокорреляционная функция описывается следующим выражением
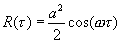
(1.13).
Для периодической функции, представимой рядом Фурье
аналогично получаем
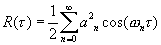
(1.14).
Таким образом, автокорреляционная функция периодической функции текущего времени t является также периодической функцией от аргумента 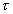 - величины временного сдвига.
- величины временного сдвига.
Носителем информации передаваемой по каналу связи или извлекаемой из эксперимента является сигнал. Наибольшее распространение получили формы реализации сигналов в виде напряжения (тока) или электромагнитного поля. Эти формы удобны как при передаче информации на большие расстояния, так и для усиления и фильтрации (селекции) сигналов.
Наряду с полезной информационной составляющей в реальном сигнале присутствуют помехи и шумы. К помехам обычно относят сигналы от других посторонних источников, «наводки» аппаратуры, машин и т.п. К шумам — случайные флуктуации, обусловленные атомизмом вещества и случайные флуктуации числа заряженных частиц в потоке, образующем электрический ток. Шум можно считать случайным процессом.
При приёме сигналов на фоне шумов встречаются следующие основные задачи:
- обнаружение полезного сигнала,
- оценка параметров сигнала,
- обеспечение минимума среднеквадратичной погрешности принятого сигнала относительно исходного
- предсказание поведения случайного сигнала на некотором последующем временном интервале.(экстраполяция).
Для решения каждой из этих задач разработаны свои «оптимальные» алгоритмы, которые основаны на стохастическом отличии поведения полезного сигнала и шума. Каждый алгоритм характеризуется своим критерием «оптимальности».
При построении таких алгоритмов используются характеристики случайного процесса, краткие сведения о них приводятся в начале . Далее в пособии рассматриваются некоторые задачи обеспечения максимального отношения сигнал / шум на выходе приёмного устройства. как для одиночных , так и периодических сигналов. Рассмотрен способ оценки параметров сигнала, принятого на фоне шума. Процессы описываются как временными , так и спектральными функциями, что соответствует методу, принятому в курсе лекций «Преобразование и генерация сигналов», частью которого данное пособие и является. Этот курс читается на третьем и четвертом семестрах на Физическом факультете Санкт-Петербургского университета. Задачи минимизации ошибки воспроизведения сигнала и экстраполяции являются содержанием специального курса для студентов радиофизиков , который читается на седьмом семестре. Эти вопросы в данном пособии не рассматриваются.
Пособие может использоваться при ознакомлении с материалом курса лекций, так и при выполнении работ в лаборатории «Радиоэлектроники» и в специальной лаборатории «Линейные системы».
![]() — мощность случайного процесса.
— мощность случайного процесса.![]() Действительно :
Действительно :![]() .
.![]()
![]() . Или
. Или![]() , беря среднее по времени от обеих частей этого равенства, получаем:
, беря среднее по времени от обеих частей этого равенства, получаем:![]() .
.![]()


![]() , убывающие как 1/T.
, убывающие как 1/T.![]()
![]()
![]()








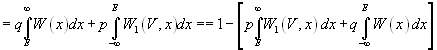 (7.4).
(7.4). 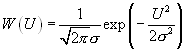 ,
, 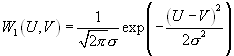
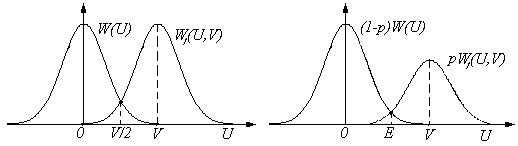
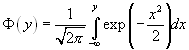 - функция Крампа [6].
- функция Крампа [6].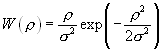 при
при 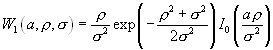 , при
, при 
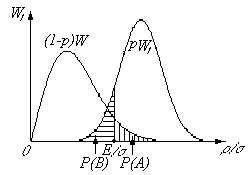
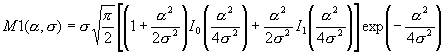 , (6.2)
, (6.2)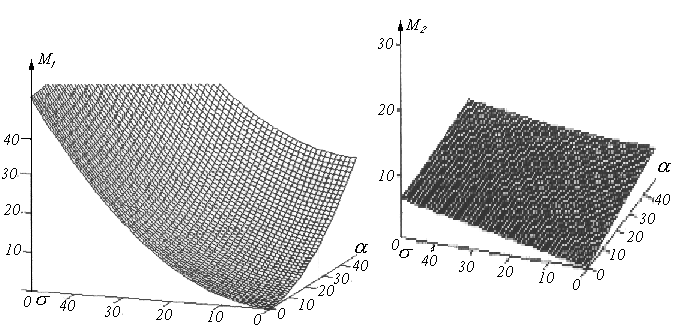
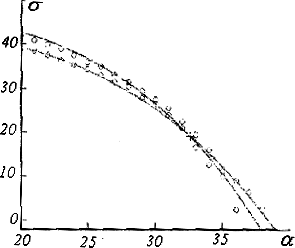
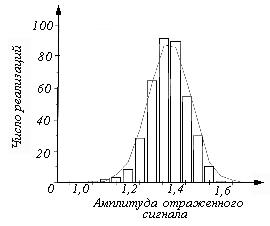
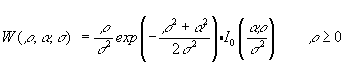 (6.1).
(6.1).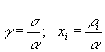 . Тогда можем записать для плотности вероятности в безразмерных величинах:
. Тогда можем записать для плотности вероятности в безразмерных величинах: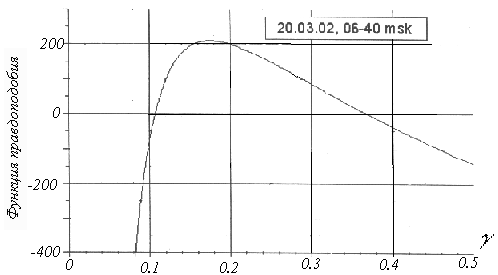
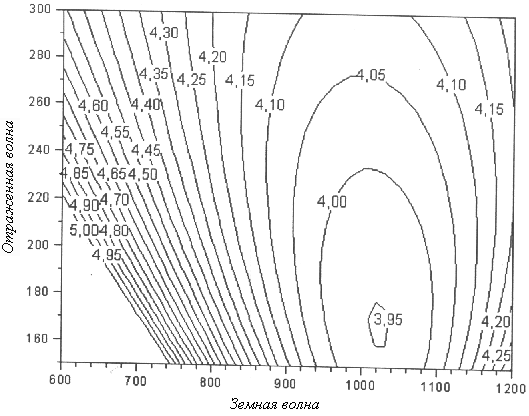

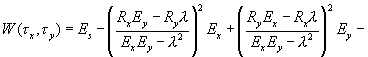
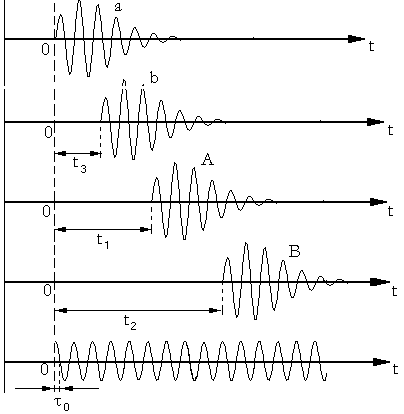
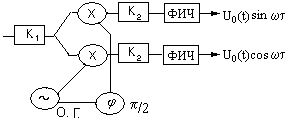
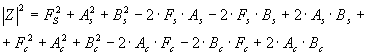 (5.11)
(5.11) (5.15)
(5.15)
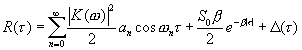 (4.5)
(4.5)
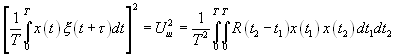 (4.9).
(4.9).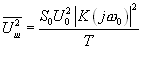 (4.10).
(4.10).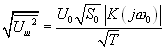 (4.11).
(4.11).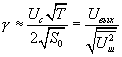 (4.13).
(4.13).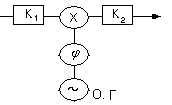
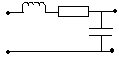
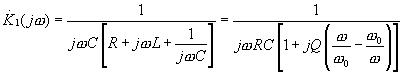 (4.14)
(4.14)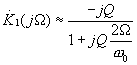 ,
, 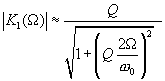 (4.15)
(4.15)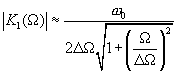 (4.16)
(4.16)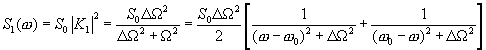 (4.18)
(4.18)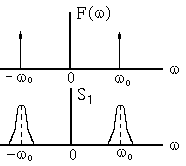
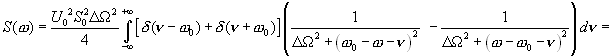
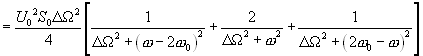 (4.23)
(4.23)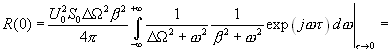
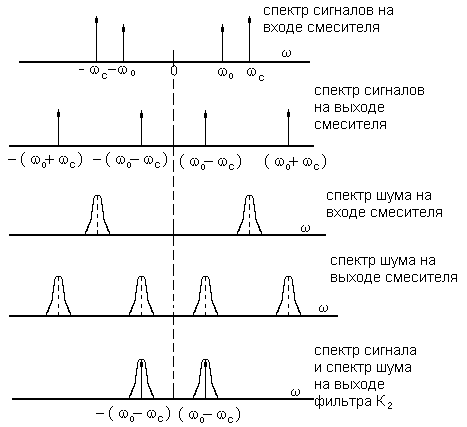
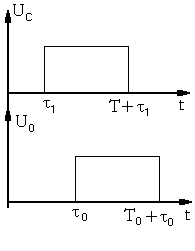
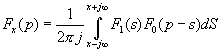 (4.32)
(4.32)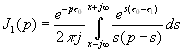 ,
, 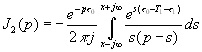
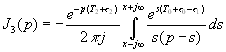 ,
, 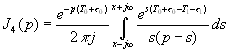 (4.33)
(4.33)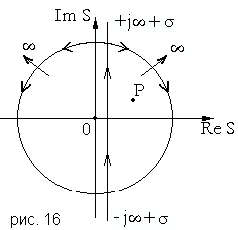
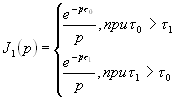
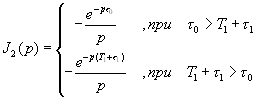
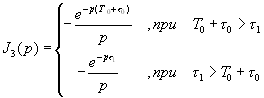
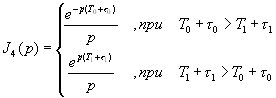
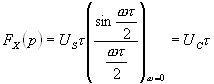 (4.35)
(4.35)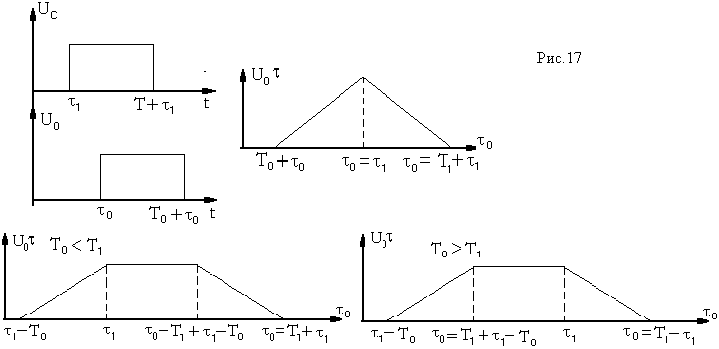
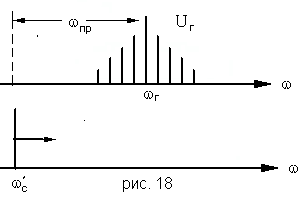
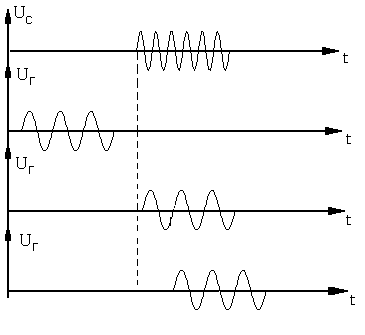
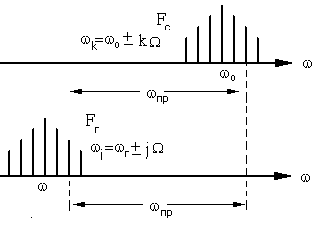
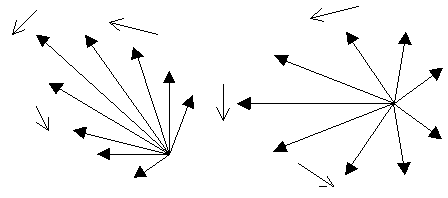
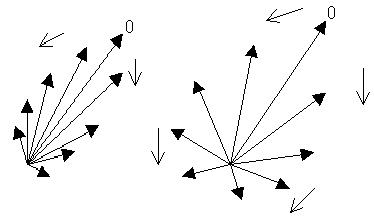
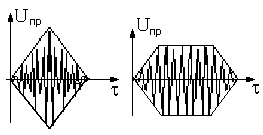

 или
или 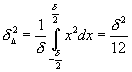
 (3.1)
(3.1)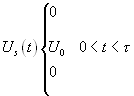 (3.4)
(3.4)
 (3.5).
(3.5).

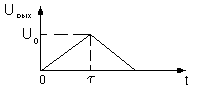
 (3.7)
(3.7) (3.8).
(3.8). (3.11).
(3.11).
 при
при (3.17)
(3.17)
 (3.18).
(3.18). (3.19).
(3.19). (3.24).
(3.24).
 (3.26).
(3.26).
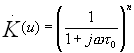
 (3.31).
(3.31).

 (3.37).
(3.37). (3.38),
(3.38), (3.39).
(3.39).